
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Чебышева (закон больших чисел)
|
|
|
|
Неравенство Чебышева
Глава 2.2. Закон больших чисел.
Рассмотрим случайную величину Х такую, что 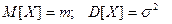 . Тогда для любого
. Тогда для любого 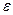 >0
>0
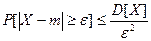 .
.
Это неравенство называется неравенством Чебышева.
Пример 3.3. Оценить вероятность того, что 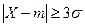 для произвольного распределения случайной величины.
для произвольного распределения случайной величины.
Решение. Пользуясь неравенством Чебышева и полагая 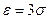 , получим:
, получим:
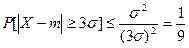 .
.
Сравнивая полученную оценку с законом трех сигм для нормального распределения, заметим, что неравенство Чебышева дает другую оценку вероятности выполнения данного соотношения. Это является следствием того, что данное неравенство верно для любого распределения случайной величины. Поэтому неравенство Чебышева не имеет практической ценности, а используется в теоретических выкладках, в частности для доказательства теоремы Чебышева.
Неравенство Чебышева можно записать в другом виде:
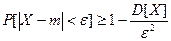 .
.
Рассмотрим последовательность случайных величин Х 1, Х 2,.., Хn. Говорят, что данная последовательность случайных величин сходится по вероятности к числу m, если для любого 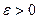
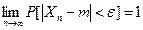 .
.
В этом случае записывают: 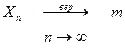 .
.
Теорема Чебышева (закон больших чисел). Если Х 1, Х 2,.., Хn – попарно независимые случайные величины, причем 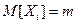 , а дисперсия
, а дисперсия 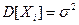 - равномерно ограниченная (то есть не превышает некоторого постоянного числа С для любого
- равномерно ограниченная (то есть не превышает некоторого постоянного числа С для любого 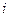 ), то
), то
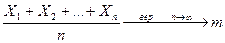 ,
,
то есть для любого 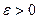
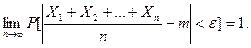
Таким образом, теорема Чебышева утверждает, что при данных условиях при достаточно большом числе случайных величин их среднее арифметическое мало отличается от математического ожидания той случайной величины, среднее арифметическое которой вычисляется.
Сущность теоремы Чебышева такова: хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значение, близкое к математическому ожиданию случайных величин, входящих в сумму.
Другими словами, отдельные случайные величины могут иметь значительный разброс, в то время как их среднее значение рассеяно мало, т.е. среднее арифметическое достаточно большого числа случайных величин утрачивает характер случайно величины.
Раздел 4. Функция одного случайного аргумента.
Система двух случайных величин.
Глава4.1. Функция одного случайного аргумента.
Если каждому значению случайной величины  соответствует одно значение случайной величины
соответствует одно значение случайной величины 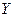 , то
, то 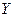 называют функцией случайной величины
называют функцией случайной величины  и записывают:
и записывают: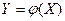 .
.
Если случайная величина  дискретная, а функция
дискретная, а функция 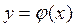 монотонная, то каждому значению случайной величины
монотонная, то каждому значению случайной величины  соответствует единственное значение случайной величины
соответствует единственное значение случайной величины 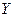 , причем вероятности соответствующих значений
, причем вероятности соответствующих значений  и
и 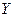 одинаковы.
одинаковы.
Пример 4.1.1. Дискретная случайная величина  имеет распределение:
имеет распределение:
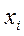
|  0 0
| 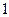
| |
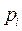
| 0,2 | 0,4 | 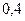
|
Найти дисперсию случайной величины 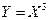 .
.
Решение:
Учитывая функциональную зависимость между двумя случайными величинами, получим закон распределения для случайной величины 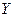 :
:
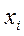
|  0 0
| 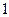
| |
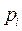
| 0,2 | 0,4 | 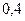
|
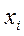
|  0 0
| 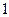
| |
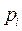
| 0,2 | 0,4 | 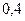
|
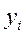
|  0 0
| 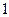
| |
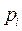
| 0,2 | 0,4 | 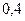
|
Тогда:
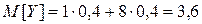 ;
; 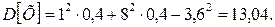 .
.
Если случайная величина  - дискретная, а функция
- дискретная, а функция 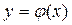 - немонотонная, то различным значениям случайной величины
- немонотонная, то различным значениям случайной величины  могут соответствовать одинаковые значения случайной величины
могут соответствовать одинаковые значения случайной величины 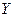 . В этом случае, для отыскания вероятностей возможных значений
. В этом случае, для отыскания вероятностей возможных значений 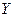 необходимо сложить вероятности тех значений
необходимо сложить вероятности тех значений  , при которых
, при которых 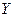 принимает одинаковые значения.
принимает одинаковые значения.
Пример 4.1.2. Случайная величина  имеет распределение:
имеет распределение:
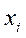
| -1 | ||
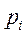
| 0,2 | 0,4 | 0,4 |
Найти закон распределения случайной величины 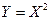 .
.
Решение: 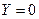 , если
, если 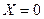 , что возможно с вероятностью 0,4.
, что возможно с вероятностью 0,4.
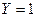 , если
, если 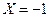 или
или 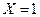 . Учитывая, что события
. Учитывая, что события 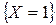 и
и 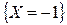 несовместны, получим:
несовместны, получим: 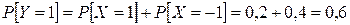 .
.
Таким образом, закон распределения случайной величины 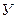 имеет вид:
имеет вид:
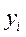
| ||
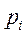
| 0,4 | 0,6 |
Если  - непрерывная случайная величина, с плотностью распределения
- непрерывная случайная величина, с плотностью распределения 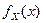 , а функция
, а функция 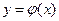 строго возрастающая или строго убывающая функция, имеющая обратную функцию
строго возрастающая или строго убывающая функция, имеющая обратную функцию 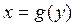 , то плотность распределения
, то плотность распределения 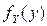 случайной величины
случайной величины 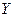 определяется формулой:
определяется формулой:
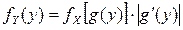 . (4.1.1)
. (4.1.1)
Пример 4.1.3: Случайная величина  распределена по закону Коши
распределена по закону Коши 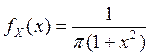 . Найти распределение случайной величины
. Найти распределение случайной величины 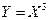 .
.
Решение: Функция 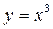 монотонно возрастающая на всей числовой оси функция, для которой обратной является функция
монотонно возрастающая на всей числовой оси функция, для которой обратной является функция 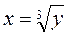 , причем
, причем 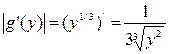 . Тогда, пользуясь формулой (4.1.1), получим:
. Тогда, пользуясь формулой (4.1.1), получим:
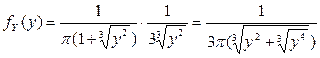 .
.
В случае если 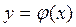 в интервале возможных значений
в интервале возможных значений  немонотонна, следует разбить этот интервал значений случайной величины
немонотонна, следует разбить этот интервал значений случайной величины  на подынтервалы, в которых функция
на подынтервалы, в которых функция 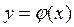 монотонна, и найти плотности распределения
монотонна, и найти плотности распределения 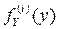 для каждого подынтервала, пользуясь формулой (4.1), а затем представить
для каждого подынтервала, пользуясь формулой (4.1), а затем представить 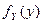 в виде суммы плотностей
в виде суммы плотностей 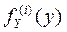 :
: 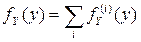 , где
, где 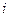 - число интервалов монотонности.
- число интервалов монотонности.
Пример 4.1.4. Случайная величина  распределена равномерно в интервале
распределена равномерно в интервале 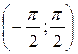 :
: 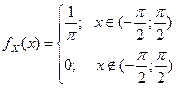 .
.
Найти распределение случайной величины 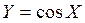 (рис. 4.1).
(рис. 4.1).
Решение:
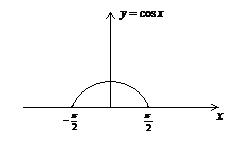
Рис. 4.1.1.
Заметим, что случайная величина 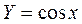 может принимать значения, принадлежащие отрезку [0;1]. Разобьем интервал значений случайной величины
может принимать значения, принадлежащие отрезку [0;1]. Разобьем интервал значений случайной величины  на котором плотность ее распределения
на котором плотность ее распределения 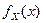 отлична от нуля, на два подынтервала, где функция
отлична от нуля, на два подынтервала, где функция 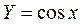 монотонна:
монотонна:
1. 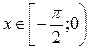 . На этом интервале функция
. На этом интервале функция 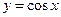 возрастает и имеет обратную функцию
возрастает и имеет обратную функцию 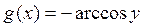 , причем
, причем 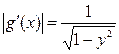 .
.
Тогда 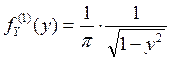 .
.
2. 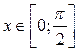 . Функция
. Функция 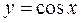 убывает,
убывает, 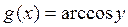 ,
, 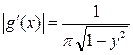 и
и 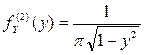 .
.
Тогда 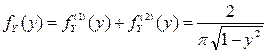 .
.
Окончательно: 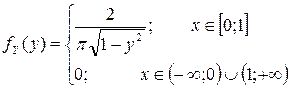 .
.
Контроль:
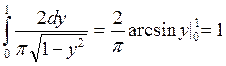
|
|
|
|
Дата добавления: 2013-12-11; Просмотров: 568; Нарушение авторских прав?; Мы поможем в написании вашей работы!