Циркуляция вектора индукции магнитного поля в вакууме

Аналогично циркуляции вектора напряженности электростатического поля в магнитном поле вводится понятие циркуляции вектора
магнитной индукции по заданному замкнутому контуру:

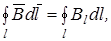
где 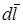– вектор элементарной длины контура, направленный вдоль обхода контура; – составляющая вектора 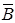в направлении к касательной к контуру с учетом выбранного обхода контура; 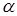– угол между векторам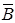и и .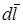

Теорема о циркуляции вектора 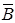или закон полного тока для магнитного поля в вакууме формулируется следующим образом: циркуляция вектора 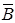по произвольному замкнутому контуру равна произведению магнитной
постоянной на алгебраическую сумму токов, охватываемых этим контуром, то есть

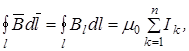(3.19)

где n – число проводников с токами,
охватываемых контуром l произвольной формы.

Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением
обхода контура правилом правого винта; ток противоположного направления считается отрицательным. Например, для системы токов, охваченных контуром l на рис. 3.9, закон полного тока
запишется следующим образом:

Выражение (3.19) справедливо только для магнитного поля в вакууме, так как для поля в веществе необходимо дополнительно учитывать молекулярные токи (микротоки).

Убедимся в справедливости теоремы о циркуляции вектора 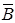на примере магнитного поля прямого тока I, перпендикулярного плоскости чертежа и направленного «к нам» (рис. 3.10).

Представим себе замкнутый контур l в виде окружности радиуса r. В каждой точке этой окружности вектор 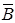одинаков по модулю и направлен по касательной к ней. Следовательно, в данном случае циркуляция вектор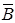а равна

Согласно выражению (3.19), получим:

или

что полностью согласуется с выражением для индукции магнитного поля прямого тока, выведенным на основе закона Био-Савара-Лапласа.

Сравнивая выражения и для циркуляции
векторов 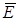и 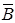, видим, что между ними существует принципиальное
различие: циркуляция вектора напряженности электростатического поля всегда равна нулю, то есть такое поле является потенциальным; циркуляция вектора 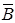отлична от нуля, поэтому магнитное поле является вихревым.

Теорема о циркуляции вектора 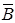позволяет находить магнитную индукцию поля без применения закона Био-Савара-Лапласа.

Дата добавления: 2013-12-12