Теорема Гаусса для магнитного поля в вакууме

Потоком вектора магнитной индукции или магнитным потоком сквозь малую поверхность площадью dS называется скалярная физическая величина, равная

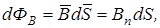(3.20)

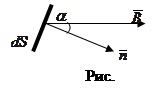где 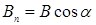– проекция вектора 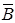на направление нормали к площадке dS (рис. 3.11); 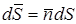– вектор, модуль которого равен dS, а направление совпадает с направлением нормали 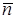к площадке.

Магнитный поток сквозь произвольную поверхность площадью S равен

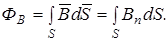(3.21)

Если магнитное поле однородно, а поверхность плоская, то как частный случай

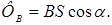(3.22)

Если плоская поверхность расположена перпендикулярно вектору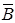, то угол 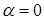и

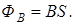
Отсюда определяется единица магнитного потока вебер (Вб): 1 Вб – это магнитный поток, проходящий сквозь плоскую поверхность площадью 1 м², расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл, то есть

1 Вб = 1 Тл·м².

Теорема Гаусса для магнитного поля формулируется следующим образом: поток вектора магнитной индукции сквозь произвольную замкнутую поверхность равен нулю:

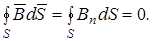(3.23)

Эта теорема отражает тот факт, что в природе не существует магнитных масс (магнитных зарядов) – источников магнитного поля, на которых начинались бы или заканчивались линии магнитной индукции. Вследствие этого линии магнитного поля не имеют ни начала, ни конца и являются замкнутыми.

Итак, потоки векторов 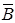и 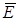сквозь замкнутую поверхность в вихревом и потенциальном полях имеют различные выражения:

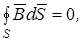
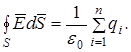
Магнитный поток через поверхность, ограниченную замкнутым контуром, называется потокосцеплением 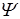этого контура. Например, потокосцепление катушки, состоящей из N витков, магнитные потоки через которые
одинаковы и равны Ф, определяется как

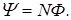
Потокосцепление контура, обусловленное магнитным полем тока в самом этом контуре, называется потокосцеплением самоиндукции. Потокосцепление контура, обусловленное магнитным полем тока, идущим в другом контуре, называется потокосцеплением взаимной индукции этих двух контуров.

В качестве примера найдем потокосцепление самоиндукции соленоида:

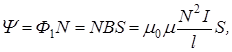
где 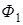– магнитный поток через один виток соленоида площадью S.

Тема 15. Вещество в магнитном поле

Не все вещества одинаково проводят линии индукции магнитного поля. Так, например, через железо магнитные линии проходят во много раз легче, чем через воздух. Другими словами способность железа проводить магнитный поток больше, чем окружающего воздуха, поэтому индукция магнитного поля в железе больше, чем в воздухе.

Величина, характеризующая магнитные свойства среды, в которой действует магнитное поле, называется магнитной проницаемостью (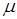). Она показывает, во сколько раз магнитная индукция В в однородной изотропной среде больше (или меньше), чем в вакууме:

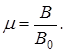
Для вакуума 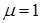. Если магнитная проницаемость какого-либо вещества меньше единицы, то это вещество называют диамагнитным. В таких
веществах магнитное поле слабее, чем в вакууме при прочих равных условиях. К диамагнитным материалам относятся медь, серебро, углерод и другие (табл. 3.1).

Таблица 3.1

Вещество	μ	Вещество	μ
Водород (газообразный)	0,999937	Серебро	0,999981
Вода	0,999991	Золото	0,999963
Стекло	0,999987	Медь	0,999912
Цинк	0,999991	Висмут	0,999824

Если магнитная проницаемость вещества больше единицы, то такое
вещество называют парамагнитным. Парамагнитными материалами являются вольфрам, платина, марганец и другие (табл. 3.2).

Таблица 3.2

Вещество	μ	Вещество	μ
Азот (газообразный)	1,000013	Эбонит	1,000014
Воздух (газообразный)	1,000038	Алюминий	1,000023
Кислород (газообразный)	1,000017	Вольфрам	1,000253
Кислород (жидкий)	1,003400	Платина	1,000253

Если магнитная проницаемость материала больше единицы во много раз, то такие материалы называют ферромагнитными (железо, никель, кобальт, некоторые сплавы). Эти материалы широко применяются в электротехнике, так как только их можно намагничивать.

Для объяснения магнитных свойств различных веществ рассмотрим
механизм действия магнитного поля на движущиеся заряды (электроны)
в атомах и молекулах вещества.

Электрон, вращающийся вокруг ядра атома по замкнутой орбите, представляет собой электрический ток (рис. 3.12). Вследствие этого возникает магнитное поле и движение электрона можно охарактеризовать орбитальным магнитным моментом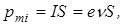

где 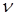– частота вращения электрона по орбите; S – площадь орбиты. Вектор 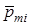направлен в соответствии с правилом правого винта.

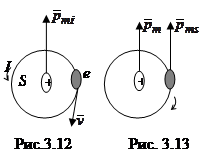Вектор орбитального магнитного момента атома 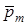равен геометрической сумме орбитальных моментов 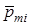отдельных электронов этого атома, то есть

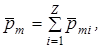
где Z – порядковый номер химического элемента в таблице Д.И. Менделеева.

Если вещество имеет молекулярное строение, то орбитальный магнитный момент молекулы равен векторной сумме орбитальных магнитных моментов атомов, входящих в состав молекулы.

Независимо от орбитального движения электроны являются источниками магнитного поля, так как вращаются вокруг собственной оси, то есть обладают собственным механическим моментом импульса – спином, и, как следствие, собственным (спиновым) магнитным моментом 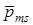. Проекция вектора 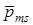на направление вектора 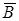может иметь одно из двух значений:

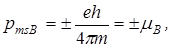
где 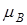– магнетон Бора.

Таким образом, магнетизм атомов обусловлен двумя причинами: движением электронов по орбитам вокруг ядра и собственным моментом импульса (рис. 3.13).

Если поместить вещество во внешнее магнитное поле, происходит
упорядочение направлений векторов магнитных моментов 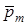отдельных атомов или молекул (намагничивание). В результате макроскопический объем магнетика приобретает определенный суммарный магнитный момент. Векторная физическая величина, определяемая магнитным моментом единицы объема вещества, называется намагниченностью:

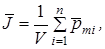
где n – число атомов или молекул в объеме V.

У большинства атомов диамагнетиков нет собственного магнитного момента, его магнитный момент индуцирован внешним полем (подобно тому, как появляется электрический момент в неполярных диэлектриках). Учитывая, что наведенный магнитный момент пропорционален индукции внешнего поля 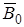, можно записать (по аналогии с диэлектриком)

,

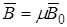где в данном случае .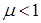

Наведенные составляющие магнитных полей атомов (молекул) складываются и образуют собственное магнитное поле 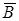вещества, ослабляющее внешнее магнитное поле. Этот эффект называют диамагнитным эффектом. Таким образом, диамагнетики – вещества, намагничивающиеся во внешнем магнитном поле против направления поля.

Диамагнитный эффект не зависит от температуры, так как тепловое движение атомов не нарушает ориентации индуцированных токов внутри атомов. Диамагнитный эффект присущ практически любому веществу.

Молекулы парамагнетиков имеют отличные от нуля собственные магнитные моменты. В отсутствие внешнего магнитного поля эти моменты расположены хаотически, поэтому вектор намагничивания равен нулю.

При внесении парамагнетика в магнитное поле магнитные моменты
отдельных атомов или молекул преимущественно ориентируются по полю. Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называют парамагнитным эффектом.

Тепловое движение атомов и молекул нарушает взаимную ориентацию магнитных моментов молекул, поэтому парамагнитный эффект зависит от температуры и 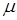парамагнетиков убывает с увеличением температуры.

Предельным случаем парамагнетизма является ферромагнетизм. Его объяснение дается в квантовой теории, где показано, что в системе, состоящей из большого количества молекул, магнитные моменты которых обусловлены спинами электронов, действуют обменные силы, стремящиеся одинаково ориентировать спины двух соседних атомов (молекул). Поэтому в некоторых веществах (железо, сталь, кобальт, никель, их сплавы) возникают
микроскопические области, имеющие вследствие сложения спинов электронов значительные магнитные моменты, то есть самопроизвольно намагниченные до насыщения. Эти области получили название доменов.

При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированы хаотически и компенсируют друг друга,
поэтому результирующий магнитный момент ферромагнетика равен нулю (вещество не намагничено). При внесении ферромагнетика во внешнее
магнитное поле происходит ориентация по полю магнитных моментов
не отдельных атомов, как у парамагнетиков, а целых областей спонтанной намагниченности.

При возрастании температуры намагничивание ферромагнетиков уменьшается, они теряют свои магнитные свойства и превращаются в парамагнитные вещества. Для каждого ферромагнитного материала есть определенная температура перехода, называемая точкой Кюри. Например, для железа 1043К, кобальта 1393К, никеля 631 К.

Характерная особенность ферромагнетиков состоит в том, что для них зависимость 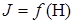, а значит, и 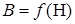является нелинейной и определяется предысторией намагничивания вещества. Это явление называют магнитным гистерезисом.

-Н

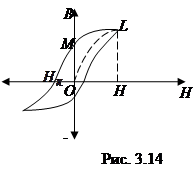При намагничивании магнитное поле внутри ферромагнетика возрастает от нуля до некоторого значения Н (рис. 3.14). Изменение значения индукции в веществе характеризуется кривой ОL. Если уменьшать напряженность поля Н, то изменение индукции изобразится кривой LM, то есть индукция ферромагнетика будет уменьшаться, но ее значения будут большими для соответствующих значений напряженности внешнего поля при намагничивании. При напряженности поля Н= 0 индукция отлична от нуля, то есть в этом состоянии (отрезок ОМ) ферромагнетик является постоянным магнитом. Чтобы уничтожить остаточное намагничивание, необходимо создать поле –Н, направленное противоположно первоначальному. Напряженность магнитного поля, при которой В= 0, называется задерживающей, или коэрцитивной, силой Н_к. При последующем изменении поля индукция также изменяется, образуя петлю гистерезиса.

В зависимости от значения задерживающей силы различают мягкие
и жесткие ферромагнетики.

Мягкие ферромагнетики имеют узкую петлю гистерезиса и малые значения коэрцитивной силы. К ним относятся железо, пермаллой и некоторые другие материалы. Из мягких ферромагнетиков изготавливают сердечники трансформаторов, генераторов и двигателей.

Жесткие ферромагнетики характеризуются широкой петлей гистерезиса и соответственно большими значениями коэрцитивной силы. К ним относятся сталь и ее сплавы. Жесткие ферромагнетики используются для изготовления постоянных магнитов.

Площадь петли гистерезиса характеризует ту работу, которую необходимо совершить для перемагничивания ферромагнетика.

Тема 16. Явление электромагнитной индукции

Как отмечалось, вокруг любого проводника с электрическим током
возникает магнитное поле. Английский физик М. Фарадей считал, что между электрическими и магнитными явлениями существует тесная взаимосвязь: раз вокруг проводника с током возникает магнитное поле, то должно иметь место и обратное явление – возникновение электрического тока в замкнутом проводнике под действием магнитного поля.

В 1831 г. М. Фарадей экспериментально обнаружил, что при изменении магнитного потока, пронизывающего замкнутый контур, в нем возникает электрический ток. Это явление было названо электромагнитной индукцией («индукция» означает «наведение»).

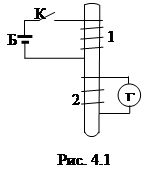
В одном из первых опытов на немагнитном стержне помещались две изолированные друг от друга медные спирали (рис. 4.1). Концы одной из них (1) через ключ К присоединялись к гальванической батарее Б, концы
другой (2) – к гальванометру Г, регистрирующему слабые токи. При неизменной силе тока I ₁ в первой спирали гальванометр показывал I ₂ = 0. Однако при замыкании и размыкании ключа К стрелка гальванометра слегка отклонялась, а затем быстро возвращалась
в исходное положение. Значит, в спирали 2 возникал кратковременный электрический ток, который был назван индукционным. Причиной возникновения индукционного тока I ₂ является изменение магнитного поля, пронизывающего спираль 2. Направления индукционного тока при замыкании и размыкании ключа были противоположными.

Явление электромагнитной индукции можно наблюдать и тогда, когда
в магнитном поле, образовавшемся между полюсами постоянного магнита, перемещается замкнутый проводник. Если этот проводник находится в покое, то в нем никакого тока не будет. Но стоит только сдвинуть его с места и перемещать так, чтобы он пересекал силовые линии магнитного поля, как тотчас же в проводнике появится электродвижущая сила и как следствие – индукционный ток. В данном случае индукционный ток возникает в проводнике за счет той механической энергии, которая затрачивается при перемещении проводника в магнитном поле. При этом механическая энергия преобразуется в энергию электрическую.

После многочисленных опытов Фарадей установил, что в замкнутом проводящем контуре индукционный ток возникает лишь в тех случаях, когда он находится в переменном магнитном поле, независимо от того, каким способом достигается изменение во времени потока индукции
магнитного поля. Обобщая результаты экспериментов, Фарадей пришел к количественному описанию явления электромагнитной индукции. Он показал, что при изменении сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение тока указывает на наличие в цепи электродвижущей силы. Значение ЭДС электромагнитной индукции 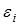определяется скоростью изменения магнитного потока:

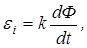(4.1)

где k – коэффициент пропорциональности.

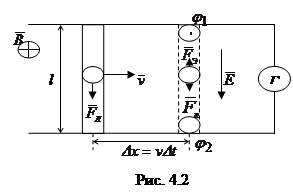Рассмотрим, как возникает ЭДС индукции, а, следовательно, индукционный ток. Пусть проводник без тока длиной l движется
в магнитном поле с индукцией 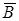со скоростью 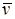(рис. 4.2). При движении проводника его свободные электроны также будут двигаться вправо, то есть возникает конвекционный ток. На каждый свободный электрон со стороны магнитного поля действует сила Лоренца 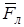. Под ее действием электроны накапливаются в нижней части проводника; соответственно положительные ионы будут накапливаться в верхней части и по концам проводника возникает разность потенциалов 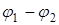. Образуется электрическое поле напряженностью 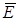, препятствующее дальнейшему перемещению электронов. Это перемещение прекратится, когда 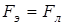, то есть 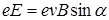, или 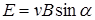. С другой стороны, 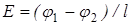, то есть .

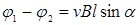Если проводник замкнуть, то в цепи потечет электрический ток. Таким образом, в проводнике индуцируется ЭДС

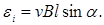(4.2)

В рассматриваемом случае 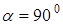, поэтому .

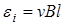Профессор Петербургского университета Э.Х. Ленц исследовал связь между направлением индукционного тока и характером вызвавшего его
изменения магнитного потока. В 1833 г. он установил закон, известный, как правило Ленца: при всяком изменении магнитного потока сквозь замкнутый проводящий контур в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению внешнего магнитного потока.

Объединив закон Фарадея и правило Ленца, получим основной закон электротехники – закон электромагнитной индукции:

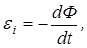(4.3)

то есть ЭДС электромагнитной индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.

Направление ЭДС индукции, а, следовательно, и индукционного тока
в проводнике, который перемещается в магнитном поле, можно также
определить, пользуясь правилом правой руки. Это правило можно сформулировать следующим образом: если ладонь правой руки расположить так, чтобы силовые линии магнитного поля были ей перпендикулярны и входили в нее, а отогнутый большой палец указывал направление перемещения проводника, то остальные вытянутые пальцы укажут направление индукционного тока в проводнике.

Как показано выше, возбуждение ЭДС индукции при движении контура в постоянном магнитном поле объясняется действием силы Лоренца, возникающей при перемещении проводника. Вместе с тем согласно закону Фарадея, возникновение индукционного тока возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае ею нельзя объяснить возникновение ЭДС электромагнитной индукции.

Для объяснения ЭДС индукции в неподвижных проводниках Максвелл предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. В этом случае проводник является лишь индикатором индуцированного (вихревого) электрического поля: поле приводит в движение свободные электроны проводника и тем самым обнаруживает себя.

Таким образом, сущность явления электромагнитной индукции заключается не столько в появлении индукционного тока, сколько в возникновении вихревого электрического поля, являющегося носителем энергии. Это является одним из фундаментальных положений электродинамики.

В отличие от электростатического поля индуцированное электрическое поле является непотенциальным, так как работа, совершаемая в вихревом электрическом поле при перемещении единичного положительного заряда по замкнутому контуру L, равна не нулю, а ЭДС электромагнитной индукции

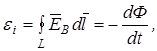(4.4)

где 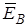– вектор напряженности индуцированного электрического поля.

Так как вихревое электрическое поле объективно существует и в отсутствие проводника, то его можно применять для ускорения заряженных частиц до скоростей, соизмеримых со скоростью света. На использовании этого принципа основано действие ускорителей электронов – бетатронов.

Дата добавления: 2013-12-12