Давление и плотность

Изменение давления и плотности движущего газа можно выразить через изменение температуры. Используя уравнение изоэнтропического процесса,

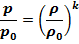
и подставив в него уравнение состояни среды, получим новое уравнение через изменение температуры:

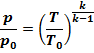
или

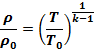
Затем подставим их в исходное уравнение изменения температуры при торможении потока

,

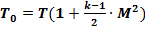С учетом этого получим формулы для определение остальных параметров газа с учетом сжимаемости

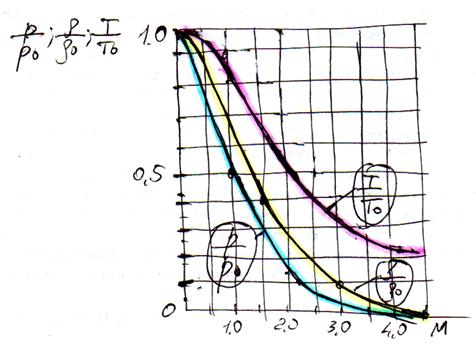
Рис 3.1.4 Схема графика зависимостей параметров потока от числа М

По мере увеличения скорости потока происходит уменьшение скорости звука в нем. Так как скорость звука уменьшается из-за уменьшения Т потока,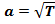, то можно установить зависимость между скоростью звука и предельной скоростью потока

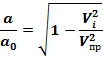
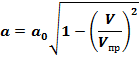
По мере роста скорости потока и уменьшения скорости звука их значение постепен-но сближаются и в некотором сечении профиля, примерно в месте максимальной толщи-ны, они сравниваются. Это сечение называется критическим.

Насколько близка 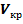и 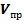– проследим на уравнении Д. Бернулли.

Запишем уравнение Д. Бернулли для критического сечения, где 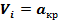, а скорость при этом равна предельной V_i=V_ПР ^, тогда 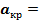V_ПР

Уравнение Бернулли для сжимаемого потока через скорость звука, когда: V_пр=a_кр имеет вид:

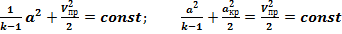, тогда получим

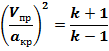
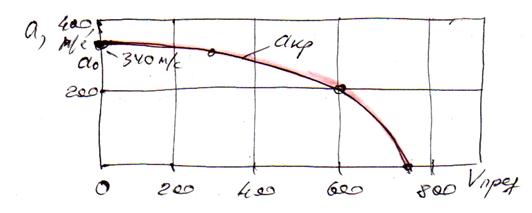
Рис 3.1.5 Зависимость скорости звука от предельной скорости потока

,

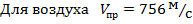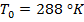
Так как при критической скорости движения 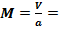1, то критические значения пара-метров потока можно определить:

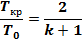
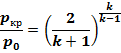
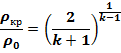
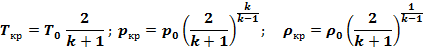
Для воздуха, при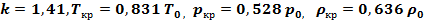

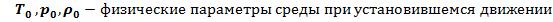
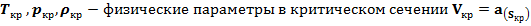
ЛЕКЦИЯ 3.2 УРАВНЕНИЕ Л. ЭЙЛЕРА С УЧЕТОМ СЖИМАЕМОСТИ.

ТЕОРИЯ СОПЛА ЛАВАЛЯ

План:

Дата добавления: 2013-12-12