Особенности определения аэродинамических характеристик профиля крыла при гиперзвуковых скоростях потока

Для приближенного расчета распределения давления по поверхности твердого тела при гиперзвуковом обтекании используется гипотеза И.Ньюто-на о корпускулярной теории гидродинамического сопротивления. Согласно этой теории частицы набегающего потока остаются невозмущенными до соу-дарения с поверхностью твердого обтекаемого тела. При ударе частицы теря-ют нормальную составляющую своего количества движения и далее движут-ся по касательной к поверхности тела. Нормальная же составляющая количе-ства движения создает импульс силы давления, которая действует на поверх-ность обтекаемого тела:

p-p_∞ = ρ_∞ V_∞² Sin²Ɵ

где

Ɵ- угол между касательной линией к поверхности обтекаемого тела и вектором набегающего потока, рад.

Таким образом, через единицу площади, параллельной наклонной плос-кости обтекаемого тела за единицу времени проходит определенная масса воздуха:

m = ρ_∞ V_∞ Sin Ɵ

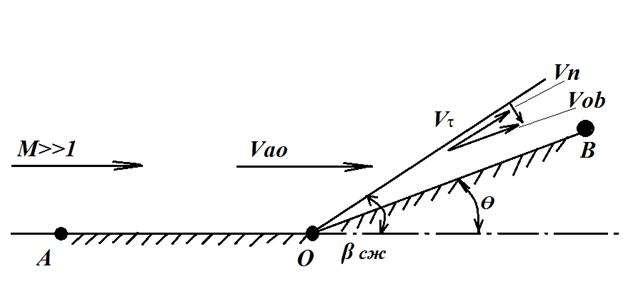
Рис. 6.3.6 Схема обтекания внутреннего угла гиперзвуковым потоком

Коэффициент давления можно определить по формуле:

p-p _∞/ q= 2 Sin²Ɵ

где

p-p _∞/ q= p

Тогда для тонких тел, когда угол наклона скачка равен углу наклона по-верхностиобтекаемого тела β = Ɵ, относительное давление равно:

p = 2Ɵ²

Применение этой формулы при гиперзвуковом течении обусловлена тем, что головная ударная волна достигает поверхности обтекаемого тела.

Расчет силы давления по формуле Ньютона достаточно точно описывает гиперзвуковое течение вокруг тела в предельных граничных условиях:

k = Cp/Cw =1 и М∞ = ∞.

Для этого случая коэффициент давления в критической точке торможе-ния считается равным:

p_макс = 2

В ходе экспериментов установлено, что при:

k = 1,33 и М∞ = 15, p_макс = 1,75

Учитывая, что в общем случае скачок не совмещается с поверхностью обтекаемого тела, то формула расчета давления имеет вид:

p = p_макс Sin²Ɵ

где

p_макс - давление в критической точке обтекаемого тела;

Поэтому расчетную формулу можно преобразовать:

p = p_∞(1 + 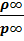V_∞² Sin²Ɵ)

Учитывая, что а² = k 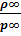, а M_∞² = V_∞² /a_∞², получим формулу для расчета давления по поверхности обтекаемого тела в виде:

p = p_∞(1 + k M_∞² Sin²Ɵ)

Согласно теории Ньютона давление на элементарную площадку обтека-емого тела зависит от положения этой площадки относительно набегающего потока и не зависит от формы остальной части тела. Поэтому сопротивление тела определяется только формой его головной части, так как только она сталкивается с частичками набегающего потока. Давление в кормой части обтекаемого тела равно нулю.

Из рассмотренного можно сделать вывод, что в гиперзвуковом потоке коэффициент давления за скачком уплотнения, при малых углах поворота потока Ɵ, пропорционален Ɵ². Аналогичным образом можно определить дру-гие физические параметры газа за косым скачком уплотнения при гиперзву-ковых скоростях течения.

Так при угле атаки α = 0, коэффициентволнового сопротивления будет равен:

Сх_а,_в = 2 Sin²β

Для получения суммарного коэффициента сопротивления, необходимо сложить коэффициенты волнового сопротивления и сопротивления трения.

При течении с расширениями потока поворот и разгон сверхзвукового потока происходит на одной характеристике ОС

Коэфициент давления равняется выражению:

p=2βϴ

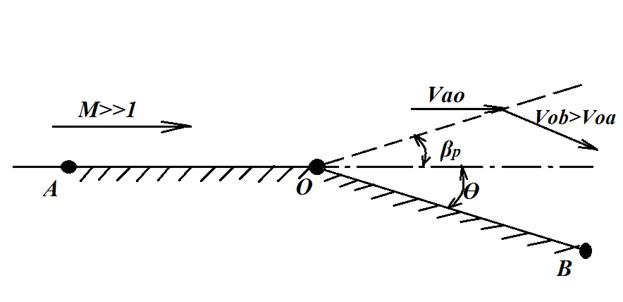
Рис 25 Схема образования характеристик расширения

Дата добавления: 2013-12-12