Общее уравнение плоскости

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Плоскость

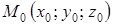Пусть дана точка и ненулевой вектор 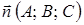(рис. 1.1). Требуется составить уравнение плоскости, проходящей через точку М ₀ перпендикулярно вектору 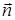(нормальный вектор плоскости).

Рассмотрим произвольную точку 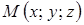этой плоскости. Так как вектор 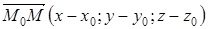лежит на плоскости, то он перпендикулярен вектору 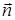. Следовательно, их скалярное произведение равно нулю

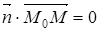(1.1)

или в координатной форме:

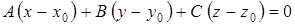(1.2)

(1.2) – уравнение плоскости, проходящей через точку 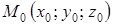перпендикулярно данному вектору .

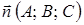Если в уравнении (1.1) в качестве нормального вектора плоскости взять единичный вектор 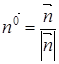, то получим так называемое нормальное уравнение плоскости

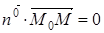. (1.3)

Введя обозначение 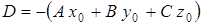, уравнение (1.2) можно переписать в виде:

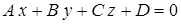, (1.4)

которое называется общим уравнением плоскости.

Следовательно, каждая плоскость в пространстве может быть задана уравнением (1.4), т.е. уравнением первой степени относительно текущих координат.

Верно и обратное: пусть в уравнении (1.4) по крайней мере один из коэффициентов А, В, С не равен нулю. Предположим, что 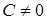. Тогда уравнение (1.4) можно переписать следующим образом:

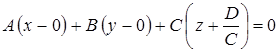. (1.5)

Уравнение (1.5) равносильно уравнению (1.4). Сравнивая уравнение (1.5) с уравнением (1.2), видим, что оно, а следовательно и равносильное ему уравнение (1.4), является уравнением плоскости, проходящей через точку 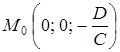и перпендикулярной вектору .

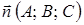Итак, всякое уравнение первой степени относительно текущих координат, т.е. всякое уравнение (1.4), определяет плоскость.

Дата добавления: 2013-12-12