Взаимное пересечение прямой и плоскости или поверхности (2 группа позиционных задач)

Вариант C. Обе плоскости общего положения

Вариант В. Одна из плоскостей проецирующая

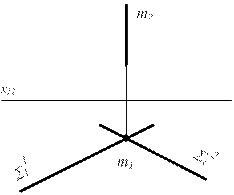
Вариант А. Обе плоскости проецирующие (рис.6.2)

а) S ¹ ^ P₁ или б) S ¹ ^ P₁

S ² ^ P₁ S ² ^ P₂

Т.к. m ÌS ¹ и S ², то единственное решение- пересечение этих плоскостей:

S ¹₁ Ç S ²₁ = m₁: для случая (а) m ^ P₁, если плоскости не параллельны; для случая (б) m₁ = S ¹₁, m₂ = S ²₂

а)	б)

Рисунок 6.2

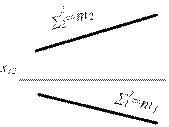
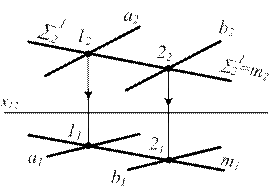
Если одна из плоскостей занимает частное положение, то ее вырожденная в прямую проекция включает в себя и проекцию линии пересечения плоскостей.

S ^1 ^ P2 S ^2 (a || b) - плоскость общего положения S ^1 Ç S ^2 = m (1; 2) { m Ì S ^1, S^ P2 }Þ m2 = S ^12 но m Î S ^2, следовательно: m Ç a = (1), m Ç b = (2) или m2 Ç a2 = (12); m2 Ç b2 = (22) Þ m2 (12; 22), а m1 (11; 21) определяется по принадлежности

Рисунок 6.3

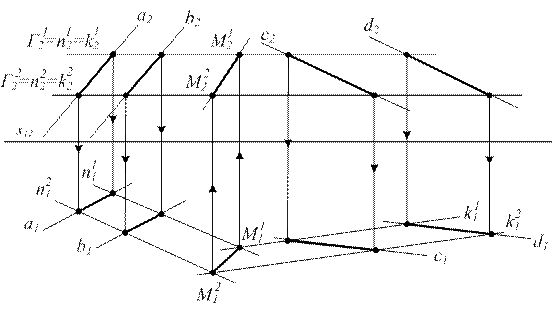
Для решения таких задач возможны два пути решения: по общему алгоритму или методом замены плоскостей проекций. Задача слишком проста для решения громоздким методом замены плоскостей проекций, поэтому решаем по общему алгоритму.

1) Вводим вспомогательную секущую плоскость Г¹. Вспомогательные плоскости всегда вводятся проецирующими: Г¹ ^ P₂ (или P₁).

2) Находим линии пересечения Г¹ с S ¹ и S ²; Г¹ Ç S ¹ =n¹; Г¹ Ç S ² = k¹.

(Это группа задач варианта В рассмотрена выше).

3) т.к. n¹ и k¹ лежат в одной плоскости Г¹, то n¹ Ç k¹ = M¹ - точка пересечения плоскостей S ¹ и S ².

Алгоритм решения повторяется: вводя вторую вспомогательную секущую плоскость Г² находим точку М². S ¹ Ç S ² = m (М¹; М²).

Рассмотрим задачу.

S ^1 (a || b) – общего положения S ^2 (c || d) – общего положения
1) Г^1 ^ P2 2) Г^1 ÇS ^1 = n^1 Г^1 ÇS ^2 = k^1 3) n^1 Ç k^1 = M^1 M^1 Î m	1) Г^2 ^ P 2) Г^2 ÇS ^1 = n^2 Г^2 ÇS ^2 = k^2 3) n^2 Ç k^2 = M^2 M^2 Î m

Рисунок 6.4

а Ç S = М

Дата добавления: 2013-12-12