
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Соосными поверхностями вращения называются поверхности, имеющие общую ось вращения
|
|
|
|
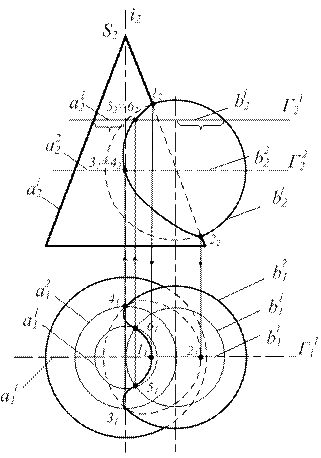
Задача.
S 1 Ç S 2 = m
S 1 - коническая поверхность вращения
S 2 - сфера.
1) G 1 || P2; G1 Î 0, G Î S
2) G1 Ç S 1 = a1
 (а12 - очерк конуса на P2)
G1 Ç S 2 = b1
(b12 - очерк сферы на P2)
3) а1 Ç b1 ={ 1, 2 }Þ
Þ (точки пересечения
очерков поверхностей на P2 ),
т. 1 и 2 гр.
1) G2 Î 0, G2 || P1
2) G2 Ç S 1 = а2
Г2 Ç S 2 = b2
3) а2 Ç b2 ={ 3,4 } Þ
точки 1 и 2 группы
1) G i || P1;
2) G i Ç S 1 = а i
G i Ç S 2 = bi;
3) аi Ç bi ={ 5,6 } Þ
Þ точки 3 группы (а12 - очерк конуса на P2)
G1 Ç S 2 = b1
(b12 - очерк сферы на P2)
3) а1 Ç b1 ={ 1, 2 }Þ
Þ (точки пересечения
очерков поверхностей на P2 ),
т. 1 и 2 гр.
1) G2 Î 0, G2 || P1
2) G2 Ç S 1 = а2
Г2 Ç S 2 = b2
3) а2 Ç b2 ={ 3,4 } Þ
точки 1 и 2 группы
1) G i || P1;
2) G i Ç S 1 = а i
G i Ç S 2 = bi;
3) аi Ç bi ={ 5,6 } Þ
Þ точки 3 группы
| 
|
Рисунок 6.15
Опорные точки (пл. Г1) 1 и 2 являются наивысшей и низшей точками линии пересечения, а также точками видимости линий на плоскости П2.
Все промежуточные точки строятся с помощью вспомогательных секущих горизонтальных плоскостей уровня Г i, расположенных равномерно между ними.
Если пересекающиеся поверхности вращения не имеют общей фронтальной плоскости симметрии, то самую высшую и самую низкую точки линии пересечения поверхностей определяют, построив изображения этих поверхностей на плоскость П4, параллельную осевой плоскости.
Вспомогательную плоскость Г2 берем на уровне экватора сферы. Полученные точки 3 и 4 определяют видимость линии пересечения относительно плоскости П1.
Графически простые линии пересечения (окружности) на данных поверхностях получаются от пересечения их горизонтальными плоскостями уровня Г i.
Вводя равномерно между наивысшей и низшей точками линии пересечения вспомогательные секущие плоскости, можно получить достаточное количество промежуточных точек построения линии пересечения.
Горизонтальная проекция линии пересечения строится по принадлежности ее точек конической поверхности.
Аналогично решаются задачи на взаимное пересечение плоскостей и поверхностей вращения из 3 группы позиционных задач (см. рис. 6.16 а-е).
а) б)
б) 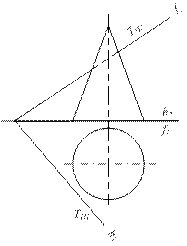
в) 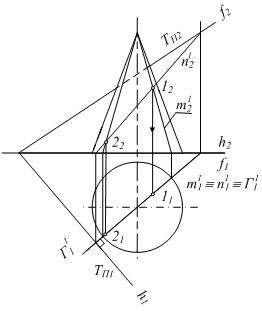 г)
г) 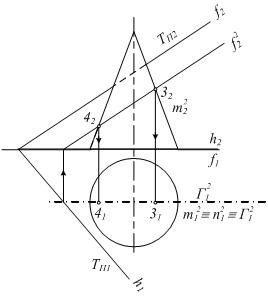
д) 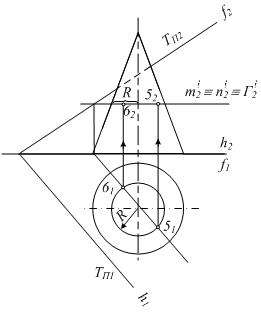 е)
е) 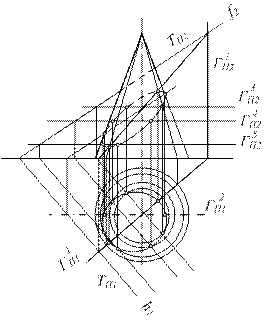
Рисунок 6.16
6.5.2 Способ концентрических сфер
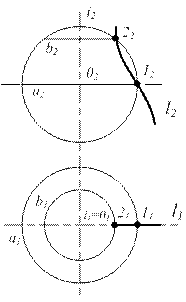
Для обоснования применения сфер, как вспомогательных секущих поверхностей, рассмотрим свойства соосных поверхностей.
Соосные поверхности вращения всегда пересекаются по окружностям, плоскости которых перпендикулярны оси вращения. Этих окружностей столько, сколько существует точек пересечения очерковых линий поверхностей.
S 1 ® поверхность вращения кривой l
S 2 ® сфера
0 Ì i;
 1 Î l Þ a Ì S 1
2 Î l Þ b Ì S 1
(a,b) = S 1 Ç S 2 1 Î l Þ a Ì S 1
2 Î l Þ b Ì S 1
(a,b) = S 1 Ç S 2
| 
|
Рисунок 6.17
Вспомогательные концентрические сферы применяются при следующих условиях:
1) обе поверхности являются поверхностями вращения;
2) оси вращения поверхностей пересекаются, они имеют общую плоскость симметрии.
i1 Ç i2 = 0, центр всех вспомогательных секущих сфер;
3) нельзя использовать способ применения вспомогательных секущих плоскостей, т.к. они не дают графически простых линий пересечения с заданными поверхностями.
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 529; Нарушение авторских прав?; Мы поможем в написании вашей работы!