Взаимное пересечение поверхностей (4 группа позиционных задач)

Вариант С. Плоскость и поверхность общего положения

Вариант В-2. Плоскость общего положения пересекается с проецирующей поверхностью

Вариант В-1. Плоскость проецирующая пересекается с поверхностью общего положения

Вариант А-2. Плоскость и поверхность являются проецирующими относительно одной плоскости проекций

Вариант А-1. Плоскость и поверхность являются проецирующими к разным плоскостям проекций

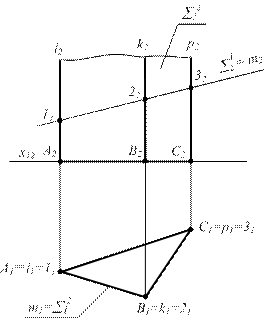
S ^1 ^ P2; S ^2 ^ P1 - призма S ^1 Ç S ^2 = m; S ^1 ^ P2 Þ m2 = S ^12 1 = l Ç S ^1 2 = k Ç S ^1 3 = p Ç S ^1 m2 = (122232) m1 = (112131) = S ^21

Рисунок 6.9

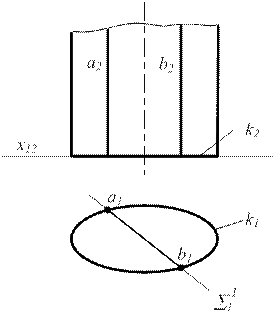
S ^1 - плоскость S ^2 - поверхность S ^1 Ç S ^2 = m ­S ^1 ^ P1 S ^2 ^ P1 - цилиндр S ^1 Ç S ^2 ={ a,b }

Рисунок 6.10

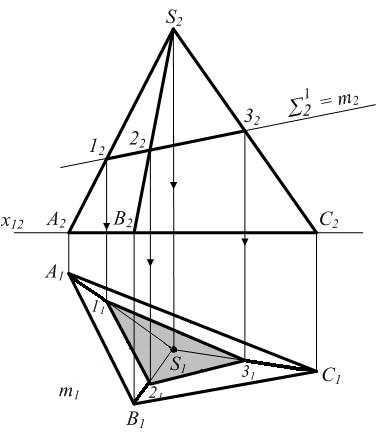
S ^1 ^ P2; S ^2 - пирамида S ^1 Ç S ^2 = m 1 = S ^1 Ç (SA) 2 = S ^1 Ç (SB) 3 = S ^1 Ç (SC) m2 = (122232) m1 = (112131) - по принадлежности m поверхности S ^2 - пирамиды

Рисунок 6.11

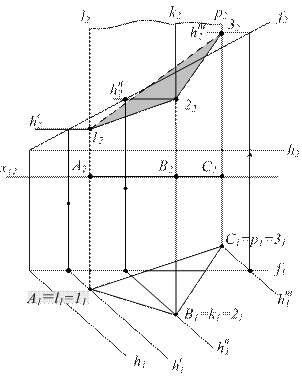
S ^1 (f Ç h) – общего положения. S ^2 ^ P1 - призма S ^1 Ç S ^2 = m (1;2;3) 1 = l Ç S ^1; l1 = 11 2 = k Ç S ^1; k1 = 21 3 = p Ç S ^1; p1 = 31 m1 = (112131). Точки сечения 1,2,3 находятся по принадлежности плоскости S(f Ç h). 11 Ì h′1; h′ Ì S h′1 || h1; 12 Ì h′2 Аналогично определяются фронтальные проекции т. 2 и 3 m2 = (12;22;32), m = [ 1;2;3 ]

Рисунок 6.12

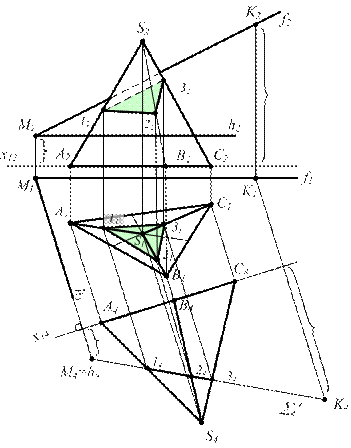
Целесообразно заменой плоскостей проекций привести к варианту В-1

S ^1 (f Ç h); S ^2 - пирамида; S ^1 Ç S ^2 = m (1;2;3) P2 ® P4 ^S ^1 Þ x14 ^ h1 ÌS ^1 1 = S ^1 Ç (SA) 2 = S ^1 Ç (SB) 3 = S ^1 Ç (SC) m4 = [ 14,24,34 ] m ÌS ^2; Þ m1 (11,21,31) и m2 (12,22,32)

Рисунок 6.13

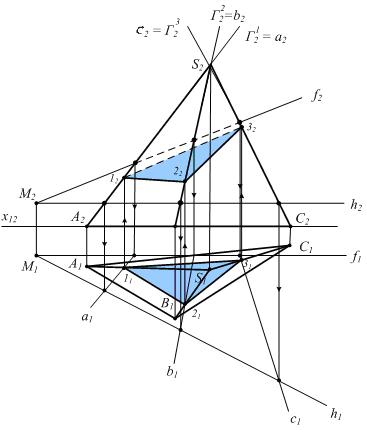
Рассмотрим решение этой же задачи по общему алгоритму. Вводим вспомогательные плоскости через ребра пирамиды.

1) Г^1 É SA; G^1 ^ P2 2) G^1 ÇS ^1 = a; (G^12 = a2) a2 Ç f2; a2 Ç h2 3) a Ç (SA) = 1 (a1 Ç S1A1) Вводим пл. Г^2 1) Г^2 É SB; Г^2 ^ P2 2) Г^2 Ç S ^1 = b; (G^22 = b2) b2 Ç f2; b2 Ç h2 3) b Ç (SB) = 2; (b1 Ç S1B1) Вводим пл. Г^3 через ребро SC и повторяем алгоритм, находим т. 3.

Рисунок 6.14

При пересечении криволинейных поверхностей или поверхностей вращения плоскостью вспомогательные плоскости вводятся через образующие поверхностей или перпендикулярно оси вращения. Найденные точки соединяются по лекалу.

В сечении цилиндрической поверхности вращения плоскостью могут быть получены следующие линии:

- окружность, если секущая плоскость перпендикулярна оси вращения цилиндрической поверхности;

- эллипс, если секущая плоскость не перпендикулярна и не параллельна оси вращения;

- две образующие прямые, если секущая плоскость параллельна оси вращения.

В сечении конической поверхности вращения плоскостью могут быть получены следующие линии:

- окружность, если секущая плоскость перпендикулярна оси вращения;

- эллипс, если секущая плоскость пересекает все образующие;

- парабола, если секущая плоскость параллельна только одной образующей;

- гипербола, если секущая плоскость параллельна двум образующим;

- две образующие прямые, если секущая плоскость проходит через вершину.

В сечении сферы плоскостью всегда получается окружность.

При решении таких задач используется метод вспомогательных секущих плоскостей, который будет рассмотрен ниже, см. рис.6.16.

Линия пересечения двух поверхностей в общем виде представляет собой пространственную кривую, которая может распадаться. При пересечении многогранных поверхностей в общем случае получается пространственная ломаная линия.

Обычно линию пересечения двух поверхностей строят по отдельным точкам. Сначала определяют опорные точки в пересечении линий очерков поверхностей. Опорные точки позволяют видеть, в каких пределах расположены проекции линии пересечения и где между ними имеет смысл определять промежуточные точки.

При этом нужно иметь в виду, что проекции линии пересечения фигур всегда располагаются в пределах площади наложения одноименных проекций очерковых линий пересекающихся поверхностей.

Общим способом построения точек линии пересечения двух поверхностей является способ вспомогательных секущих плоскостей или поверхностей. Вспомогательная плоскость или поверхность пересекает данные поверхности по графически простым линиям.

В пересечении этих линий получаются точки, принадлежащие обеим поверхностям, т.е. точки их линии пересечения. В качестве вспомогательных поверхностей обычно используются плоскости или концентрические сферы. (Концентрическими называются сферы, имеющие общий центр и различные радиусы).

Решение позиционных задач основано на применении вспомогательных секущих плоскостей или поверхностей, которые надо выбирать и располагать так, чтобы выполнялось два условия:

1) линии пересечения вспомогательной плоскости или поверхности и заданных поверхностей должны иметь вид прямых линий либо окружностей;

2) вспомогательные плоскости или поверхности располагать так, чтобы проекции линии пересечения были отрезками, прямыми либо окружностями, дугами окружностей.

Рассмотрим общий алгоритм решения:

1) Г ⁱ - вспомогательная секущая плоскость или поверхность, i =1,2,3...n;

2) Г ⁱ Ç S ⁱ = аⁱ,

G ⁱ Ç S ² = bⁱ - проекции линий пересечения a и b должны быть либо пря­мые, либо окружности;

3) аⁱ Ç bⁱ = M ⁱ Ì m - точки искомой линии пересечения поверхностей.

Все точки линии пересечения поверхностей можно разделить на 3 группы:

1 - габаритные точки каждой из проекций линии пересечения;

{ M } = 2 - точки, определяющие видимость кривой на плоскостях проекций;

3 - случайные или промежуточные точки каждой из проекций.

6.5.1 Применение вспомогательных секущих плоскостей

Дата добавления: 2013-12-12