Банковский метод дает большее наращение

Основные понятия кредитной операции

Сумма, полученная сегодня, больше той же суммы, полученной завтра

Модуль 1. Простые проценты

Золотое правило бизнеса:

В основе финансово-экономических расчетов лежит понятие временной ценности денег. В практических финансовых и коммерческих операциях суммы денег обязательно связываются с некоторыми конкретными моментами или интервалами времени. Для этого в контрактах фиксируются соответствующие сроки, даты, периодичность поступлений денежных средств или их выплат.

Фактор времени играет не менее важную роль, чем размеры денежных сумм. Необходимость учета фактора времени определяется принципом не равноценности денег, относящихся к разным периодам времени.

Дело в том, что, даже в условиях отсутствия инфляции и риска, 1000 руб., полученных через год, не равноценны этой же сумме, полученной сегодня. Не равноценность определяется тем, что любая сумма денег может быть инвестирована сегодня и принести доход в будущем. Поступившие доходы в свою очередь могут быть реинвестированы и т.д.

Следовательно, сегодняшние деньги в этом смысле ценнее будущих, а будущие поступления менее ценны, чем современные.

Известный афоризм, «время - деньги» (Time is money) как нельзя лучше выражает сущность современного количественного финансового анализа.

Расчет и анализ любой финансовой операции начинается с приведения всех платежей, осуществленных в различные моменты времени, к одному моменту (настоящему или будущему), только после этого денежные суммы можно между собой сравнивать, вычитать, складывать.

Описание изменения денежных сумм во времени производится путем вычисления дохода от инвестирования денег, т.е. путем начисления процента на первоначальную сумму, поэтому теория процентных ставок – основа временной стоимости денег.

Получение кредита – наиболее распространенная финансовая сделка. Она характеризуется следующими величинами:

K – начальный капитал или сумма ссуды;

S – наращенная сумма или полная стоимость кредита с процентами.

I = S - K – доход (процентные деньги, проценты), получаемый кредитором от предоставления денег в долг;

n – период начисления процентов в годах,

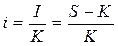, n =1 год – процентная ставка – относительная величина дохода в сумме долга за единицу времени.

Процентная ставка i может измеряться в процентах (%), в виде десятичной или натуральной дроби.

Например: i=15% =0.15;

i=200%=2.0 и т.д.

В формулах для финансовых расчетов процентная ставка берется в виде десятичной дроби.

1. По базе начисления проценты делятся на простые и сложные.

Если база постоянна на весь период начисления процентов, используют простые проценты. Обычно период начисления в этом случае n < 1 года.

Если за базу для начисления принимается сумма, полученная из предыдущей, с прибавлением к ней процентов,то используют сложные проценты (иначе, процент на процент)

2. По принципу расчета процентов различают ставки наращения i и учетные ставки d.

Плата за кредит может взиматься как в конце срока, так и в его начале.

В первом случае проценты начисляются в конце срока, исходя из величины предоставляемой суммы K, и возврату подлежит сумма долга вместе с процентами, т.е S = K + I.

Такой способ начисления процентов называется декурсивным.

Процентная ставка 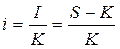, (n=1 год) называется ставкой наращения.

Во втором случае процентный доход D называемый дисконтом, выплачивается в начале срока. При этом должнику выдается сумма, уменьшенная на его величину, т.е S - D; а возврату в конце срока подлежит вся исходная ссуда S.

Такой способ начисления процентов называется антисипативным, а процентная ставка – учетной ставкой.

Учетная ставка

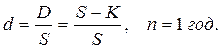
3. Процентные ставки могут быть фиксированными (постоянными), когда в контракте (сделке, финансовой операции) указывается их размер или «плавающие», когда фиксируется не сама ставка, а изменяющиеся во времени базовая ставка и надбавка к ней, называемая маржой.

4. По периоду начисления проценты делятся на дискретные проценты и непрерывные проценты.

Дискретные проценты начисляются за фиксированные в договоре интервалы времени (год, полгода, квартал, месяц, день).

Непрерывные проценты связаны с непрерывным интервалом начисления.

Операция наращения состоит в том, что по сегодняшней сумме ссуды K рассчитывается ее будущая стоимость S.

Операция дисконтирования состоит в том, что на сегодняшний момент времени пересчитывается некоторая будущая сумма денег S.

В этом случае сумму K называют современной или приведенной величиной.

Простые проценты

Простые проценты - это метод расчета дохода кредитора от предоставления денег в долг заемщику.

Сущность простых процентов состоит в том, что они начисляются на одну и ту же величину капитала К в течение всего срока ссуды. Простые проценты дают больший доход при их начислении на срок меньше года.

Основная формула простых процентов:

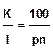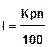или , где

К - начальный капитал,

I - доход (процентный платеж, процентные деньги или просто проценты), получаемый кредитором от заемщика за пользование денежной ссудой;

p - процентная ставка, показывающая сколько денежных единиц должен заплатить заемщик за пользование 100 ед. капитала за год,

т. е. годовая ставка в процентах. Если ставка измеряется в долях единицы, то она обозначается буквой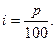

Если деньги отданы взаймы под проценты, то заемщик возвращает наращенную сумму

S = K + I = K + Kni = K(1 + ni), где

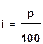- процентная ставка в долях единицы, n- время в долях года.

Доход за n лет I = Kni,

(1 + ni) - множитель наращения по простым процентам.

Итак, если по начальному капиталу (сегодняшним деньгам) K находится будущая сумма денег S, то операция называется наращением.

Если же, зная будущие деньги S, находят их сегодняшнюю сумму K по формуле: 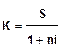, то операция называется математическим дисконтированием, 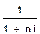- дисконтный множитель.

Задача1.

Капитал 200 тыс.руб. вложен в банк на 8 месяцев под 12% годовых.

Найти сумму, которая будет получена к концу срока.

К = 200 тыс.руб., n =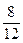года, i = 0,12, p = 12%. S =?

Решение:

I способ.

S = K + I, I = .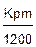

I =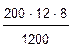= 16 тысяч руб.

S = 200 + 16 = 216 тысяч руб.

II способ.

Ставка годовая, срок n в месяцах переведем в доли года: n = 8 месяцев = 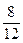года.

S = K(1 + ni)=200(1 +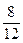.0,12) = 216 тысяч руб.

Задача 2.

Капитал 200 тыс.руб. вложен в банк на 80 дней под 12% годовых.

Найти величину вклада через 80 дней. Расчет сделать точным и банковским методом.

Решение:

K = 200 тысяч руб. n =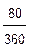года или n =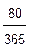года, i = 0,12, S=?

1.Точный метод:

Т.К. ставка годовая, срок n переведем в доли го да: n =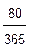года,

S = K(1 + ni) = 200(1 + 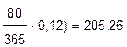тыс.руб.

1. Банковский метод:

Срок n = 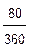года,

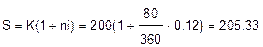тыс.руб.

Дата добавления: 2013-12-12