По определению наращенной суммы ренты

Классификация рент

1. ренты немедленные (начало срока ренты и начало действия контракта совпадают) и ренты отсроченные;

2. ренты с ежегодным начислением процентов (m=1), начислением процентов m раз в году и непрерывным начислением процентов;

3. ренты с постоянными и переменными членами;

4. ренты конечные и бесконечные. Если срок ренты более 50 лет, рента считается вечной.

5. рента обычная или постнумерандо, если платежи производятся в конце периода; рента пренумерандо, если платежи производятся в начале периода.

Пример 4-х летней ренты постнумерандо:

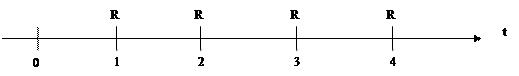Пример 4-х летней ренты пренумерандо:

Обычно анализ потока платежей предполагает расчет или наращенной суммы или современной стоимости.

Наращенная сумма S ренты

Наращенная сумма - сумма всех членов потока платежей с начисленными на них к концу срока процентами.

1. Годовая рента постнумерандо

Ее характеристики: член ренты R, срок ренты n, ставка i, число выплат в году p=1, число начислений процентов в году m=1.

Положим n=4 года и выведем формулу наращенной суммы ренты.

Построим схему наращения членов ренты на временной оси. Т.к. срок ренты больше одного года, естественно использовать сложные проценты.

Например, на член ренты R, внесенный в конце первого года, будут начисляться проценты 3 года. К концу срока ренты эта сумма будет составлять .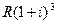

Подобным образом, на член ренты R, внесенный в конце второго года, будут начисляться проценты 2 года. К концу срока ренты эта сумма будет составлять 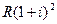. И т. д.

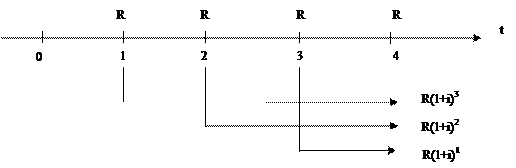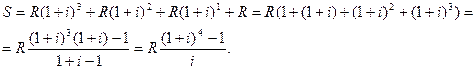
Замечание:

Воспользовались формулой возрастающей геометрической прогрессии:

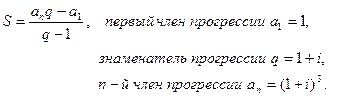
Тогда общая формула наращенной суммы ренты будет иметь вид:

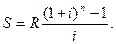
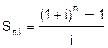- коэффициент наращения ренты, будем находить его, пользуясь математическим калькулятором.

Дата добавления: 2013-12-12