Принцип действия электрического двигателя постоянного тока

Основные элементы конструкции. Электродвигатель постоянного тока (рис. 3.2) состоит из неподвижного остова 12 с полюсами 6, предназна­ченными для создания магнитного потока, и вращающегося якоря 8, в котором происходит преобразование электрической энергии в механичес­кую. Остов 12 цилиндрической фор­мы, отлитый из стали, является частью магнитной системы электро­двигателя. На внутренней поверхности остова закреплены две или три пары полюсов. Каждый полюс 6 состоит из стального сердечника и об­мотки возбуждения 7 из изолирован­ного провода. Обмотки возбуждения полюсов соединены между собой так, что при протекании тока по этой цепи, северные N и южные S полюса чередуются (направление магнитно­го потока в полюсах и остове пока­зано на рис. 3.2 стрелками). Якорь электродвигателя 8 состоит из сталь­ного цилиндрического сердечника и коллектора 4, насаженных на вал 9. На сердечнике якоря 8 по окруж­ности располагаются продольные па­зы 13, в которых находятся изоли­рованные проводники, образующие обмотку якоря.

При работе электродвигателя по всем проводникам обмотки якоря протекают токи. Силы взаимодейст­вия этих токов с магнитным потоком полюсов вращают якорь. Обмотка якоря соединена с источником элек­троэнергии через коллектор 4, состо­ящий из радиально расположенных медных пластин, изолированных друг от друга. К каждой коллектор­ной пластине припаяны проводники обмотки якоря. Коллектор соединен с внешней цепью через угольно-гра­фитовые стержни 1, называемые щетками. Щетки установлены в непо­движных щеткодержателях 2. Под действием пружин щетки прижаты к коллектору и скользят по его цилин­дрической поверхности при враще­нии якоря. Вал якоря опирается на роликовые или шариковые подшип­ники 5 и 10, расположенные в под­шипниковых щитах 3 и 11. Щиты прикреплены болтами к остову 12.

Вращающий момент электродви­гателя. Рассмотрим электродвига­тель с двухполюсной магнитной сис­темой (рис. 3.3), в обмотке якоря которого выделены два последова­тельно соединенных проводника под­ключенные к двум пластинам коллек­тора. Как известно из курса физики, на прямолинейный проводник с то­ком находящийся в однородном магнитном поле с индукцией В_, дей­ствует сила электромагнитного разрезы электродвигателя постоянного тока

взаимодействия, определяемая законом Ампера,

3.1

где -длина участка проводника, взаимодействующего с магнитным полем; -угол между векторами В и .

Рис. 3.2. Продольный (а) и поперечные (б, в)

Векторы В и I - перпендикулярны(см. рис. 3.3) и, следовательно, .

Магнитная индукция

3.2

Отношение суммарной площади всех полюсов к площади боковой цилиндрической поверхности якоря называется коэффициентом полюсного перекрытия . Тогда площадь одного полюса

3.3

Пусть обмотка якоря состоит из N проводников и образует 2а парал­лельных ветвей. Тогда в проводнике обмотки якоря

3.4

Вращающий момент электродвигателя

3.5

где 0,5-плечо силы относительно оси якоря; N-число проводников обмотки якоря.

Подставляя в формулу (3.5) выражения (3.1), (3.2), (3.3), (3.4), получим

(3.6)

где -постоянный коэффициент, характеризующий обмотку якоря электрической машины.

Этот коэффициент

(3.7)

Рис. 3.3. Схема, поясняющая принцип работы электродвигателя постоянного тока

Изложенное позволяет сделать следующие выводы:

1. Вращающий момент электродвигателя пропорционален току и магнитному потоку.

2.Вращающий момент не имеет прямой зависимости от угловой скорости якоря. Поэтому электродвига­тель может развивать вращающий момент даже при неподвижном яко­ре, что очень важно для плавного трогания поезда с места.

3.Направление силы и, следо­вательно, направление вращения
якоря электродвигателя определя­ются по правилу левой руки. Направление вращения якоря можно изменить двумя способами: либо изменить направление тока в обмотке якоря, либо переменить на­правление магнитного потока по­люсов.

4.Направление вращения якоря можно изменить двумя способа: либо изменить направление тока в обмотке якоря, либо переменить направление магнитного потока полюсов.

Электродвижущая сила (э. д. с.) вращения. Если якорь электродвига­теля вращается, то в каждом провод­нике его обмотки индуцируется э. д. с. Е, которая определяется по закону электромагнитной индукции:

(3.8)

где - скорость движения проводника об­мотки якоря относительно магнитного поля; — угол между векторами В и v_я (так как они перпендикулярны, то sin =1).

Скорость связана с угловой ско­ростью якоря 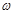известным соотно­шением

(3.9)

Направление э. д. с. 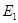определяют по правилу правой руки. Чтобы под­черкнуть причину возникновения, ее принято называть э. д. с. вращения. Как увидим далее, она определяет такие важные характеристики элек­тродвигателя, как потребляемый ток и развиваемую механическую мощ­ность.

Определим э. д. с. вращения для всей обмотки якоря. Если обмотка якоря состоит из N проводников и образует 2а параллельных ветвей, то каждая ветвь обмотки состоит из N/(2а) последовательно соединенных проводников. Тогда э. д. с., индуци­руемая во всей обмотке якоря, .

Используя выражения (3.1), (3.2), (3.8), (3.9) и имея в виду, что sin =1, получим

(3.10)

Учитывая формулу (3.7),

(3.11)

Отсюда следует, что э. д. с. враще­ния прямо пропорциональна магнит­ному потоку и угловой скорости вращения якоря.

Угловая скорость якоря электро­двигателя. Определим ее, исполь­зуя закон сохранения энергии. Элек­трическая мощность, потребляемая электродвигателем из сети,

где Р_мех — механическая мощность на валу электродвигателя; r_д — сопротивление обмо­ток электродвигателя.

Выражение представляет со­бой мощность, затраченную на нагре­вание обмоток электродвигателя.

Механическая мощность навалу электродвигателя Р_мех, как известно, равна произведению вращающего момента М на угловую скорость якоря 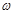. Пользуясь выражениями (3.6) и (3.11), можно доказать, что

Таким образом, э. д. с. вращения характеризует преобразование элек­трической энергии в механическую. Подставив в формулу зна­чения и , получим

(3.12)

Разделив равенство (3.12) на получим

(3.13)

Из выражения (3.13) следует, что напряжение U_д, приложенное к электродвигателю, уравновешивается суммой э. д. с. вращения Е и падения напряжения на обмотке электродви­гателя . Выражение (3.13) называют уравнением равнове­сия напряжений в цепи электродвигателя.

Для того чтобы преобразование электрической энергии в механическую было наиболее полным, необхо­димо иметь относительно малое со противление обмоток электродвигателя . С этой целью обмотки изго­товляют из проводников возможно большего сечения. У тяговых элек­тродвигателей мощностью свыше 400 кВт падение напряжения на обмотках обычно составляет около 4 % приложенного напряжения U_д, а остальные 96% приходятся на э. д. с. вращения. Таким образом, .

Формулу для определения угловой скорости якоря электродвигателя можно получить из выражений (3.11) и (3.13):

(3.14)

Из формулы (3.14) видно, что угловая скорость 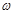возрастает при увеличении напряжения U_д, подве­денного к электродвигателю, а также при уменьшении сопротивления в цепи электродвигателя и магнит­ного потока Ф. Частота вращения вала электродвигателя, об/мин, рассчитывается по формуле

(3.15)

Номинальный режим работы элек­тродвигателя. Этот режим определя­ется нагреванием электродвигателя в процессе работы под действием потерь энергии в обмотках , а также механических и магнитных потерь, возникающих при вращении якоря. При повышении температуры, обмоток электродвигателя срок службы их изоляции значительно со­кращается. Предельно допустимая температура обмоток для различных классов изоляции лежит в пределах 160—220 °С.

Для каждого типа электродвига­теля завод-изготовитель устанавливает номинальный режим работы, при котором обмотки двигателя в течение 1 ч нагреваются до предельно допустимой температуры. Напряже­ние на электродвигателе, его мощность, потребляемый ток и частота вращения, соответствующие номи­нальному режиму, называют номи­нальными и обозначают в индексе буквой Н: ,,,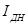. Обычно эти величины указывают на фирмен­ном щитке электродвигателя.

Режим работы электродвигателя, когда он развивает мощность больше номинальной, называется перегруз­кой. При перегрузке двигатель ин­тенсивно нагревается и может выйти из строя. Допустимые значение и длительность перегрузки устанавли­вает завод-изготовитель. Обычно до­пускается 1,5-кратная перегрузка электродвигателя в течение несколь­ких минут.

Электромеханические характерис­тики электродвигателя. Эти харак­теристики представляют собой зави­симости вращающего момента М и угловой скорости якоря ω от тока , потребляемого электродвигате­лем. Характер зависимостей М( ) и ω(), определяемый формулами (3.6) и (3.14), обусловлен способом питания обмоток возбуждения элект­родвигателя. При независимом воз­буждении обмотка полюсов получает питание от отдельного источника постоянного тока (рис. 2.12, а).

Рис. 3.4. Принципиальные схемы (а, б) и электромеханические характеристики (в, г, д) электродвигателя постоянного тока при неза­висимом (штриховые линии) и последователь­ном (сплошные линии) возбуждении.

По­скольку ток возбуждения I_в не зави­сит от тока якоря I_д, то магнитный поток полюсов электродвигателя Ф можно считать практически постоян­ным (рис. 3.4, в). Тогда вращаю­щий момент электродвигателя со­гласно формуле (3.6) прямо про­порционален току (рис. 3.4, г). Частота вращения электродвигателя определяется формулой (3.14), в ко­торой знаменатель постоянен, а чис­литель с ростом тока уменьшается незначительно. Поэтому частота вра­щения электродвигателя независи­мого возбуждения несколько снижа­ется с увеличением тока (рис. 3.4, д).

При последовательном возбужде­нии обмотки якоря и полюсов вклю­чены последовательно в общую цепь (рис. 3.4, б) и ток возбуждения равен току якоря (I_в = I_д). Этот способ возбуждения называют также сериесным (от английского Series — ряд, последовательность). При по­следовательном возбуждении маг­нитный поток полюсов Ф зависит от тока и определяется магнитны­ми свойствами стали, из которой из­готовлен остов двигателя, сердечни­ки якоря и полюсов. Зависимость Ф() подобна кривой намагничива­ния ферромагнитных материалов (см. рис. 3.4, в). При сравнительно не­больших значениях тока возбужде­ния магнитный поток Ф прямо про­порционален . При дальнейшем увеличении тока наступает магнитное насыщение стали и рост магнит­ного потока замедляется.

При ненасыщенной системе элект­родвигателя возрастание тока при­водит к пропорциональному увели­чению магнитного потока. В резуль­тате вращающий момент в соответ­ствии с формулой (3.6) возрастает пропорционально квадрату тока. При насыщении магнитной системы электродвигателя увеличение тока приводит к очень незначительному возрастанию магнитного потока. По­этому при больших токах зависимость вращающего момента от тока очень близка к линейной (см. рис. 3.4, г).

Частота вращения электродвига­теля с последовательным возбужде­нием заметно уменьшается с ростом тока якоря (см. рис. 3.4, д) главным образом вследствие увеличения маг­нитного потока Ф, входящего в зна­менатель формулы (3.14). Числитель формулы (3.14) с увеличением тока якоря уменьшается весьма незначительно.

Чтобы рассчитать ток, потребляе­мый электродвигателем, подставим значение э. д. с. вращения (формула 3.11) в уравнение равновесия напря­жений (формула 3.13). Получим

Для электродвигателя с независи­мым возбуждением магнитный поток Ф остается постоянным при измене­нии тока якоря. Найдем отсюда ток

(3.16)

Из формулы (3.16) видно, что с уменьшением частоты вращения яко­ря ток электродвигателя возрастает. Тяговые электродвигатели имеют ма­лое сопротивление обмоток. Поэтому при подключении электродвигателя с неподвижным якорем (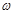 = 0) к но­минальному напряжению ток дости­гает значения, которое бо­лее чем в 10 раз превышает номи­нальный ток. Такой режим работы недопустим. Поэтому при пуске электродвигателя нужно принимать меры для ограничения пускового тока.

Электродвигатель последователь­ного возбуждения при перегрузке развивает больший вращающий мо­мент (см. рис. 3.4, г, д), а при ма­лых нагрузках — более высокую скорость движения, чем электродви­гатель с независимым возбужде­нием. Имеются и некоторые другие преимущества электродвигателей последовательного возбуждения, благодаря чему они получили широ­кое применение на современном электрическом подвижном составе. независимое возбуждение тяговых электродвигателей применяют только в особых условиях, например в режиме электрического торможения.

Дата добавления: 2013-12-12