Задачи оптимизации

Задача повышения эффективности технологических и организационных систем (например: металлорежущего станка, автоматической линии, производства в целом) путём принятия обоснованных решений актуальна во всех областях деятельности человека. Количественная оценка эффективности может быть получена при заданной цели функционирования системы, с учётом ограничений на ресурсы, привлекаемые для достижения цели. При этом задача принятия решения ставится как задача выбора параметров системы, обеспечивающих максимизацию или минимизацию целевой функции. Последняя количественно определяет степень достижения цели – величину критерия оптимизации. В качестве критерия можно принять, например, себестоимость изделия (цель-минимизация), быстродействие машины или прибора (цель-максимизация) и другие показатели.

В процессе оптимизации, с учетом заданных условий, отыскиваются элементы решения, т. е. те параметры системы и показатели качества, которые зависят от выбора и приводят к отыскиванию оптимальных конструкций, технологических схем и др.

Всякая оптимизационная задача предполагает заданной целевую функцию — количественный показатель качества альтернатив выбора. Обычно в задачах оптимизации отыскивается экстремум интегрального показателя, который представляется одной функцией f (X) нескольких переменных, заданной в некоторой области допустимых значений переменных.

Наименьшее или наибольшее значения целевой функции из всех возможных в заданной области R называются глобальными экстремумами. Значение X, при котором достигается глобальный экстремум, называется точкой глобального экстремума. Локальный экстремум функции f (X) — значение f (Х°) этой функции такое, что для любого Х из R, близкого к Х° из R, справедливо f (Х°) ≥ f (X) (локальный максимум) или f (Х°) ≤ f (X) (локальный минимум).

Обоснованное применение количественных методов для принятия решений – оптимизацию поведения структур систем называют исследованием операций (ИСО). Здесь операция – комплекс целенаправленных действий.

Задача, рассмотренная выше, решается с применением математической модели системы, объединяющей упомянутые ограничения на ресурсы и целевую функцию. Нахождение величин упомянутых параметров системы (они входят в математическую модель как неизвестные) путём решения математической задачи называют математическим программированием. Математическое программирование – важнейшая область математики, ориентированная на широкое применение компьютеров.

В зависимости от характера целевой функции, а также ограничений могут использоваться различные методы оптимизации (математического программирования): линейное программирование, нелинейное программирование (хотя бы одна из функций нелинейна по X), целочисленное линейное программирование, динамическое программированиеи др.

5.6. Задачи линейного программирования

5.6.1. Модель задачи ЛП.

Одним из разделов математического программирования является линейное программирование. В моделях линейного программирования так называемая “основная задача” состоит в нахождении неотрицательного решения системы линейных уравнений или неравенств (ограничений), которое минимизирует или максимизирует линейную форму (целевую функцию). Математическая задача линейного программирования записывается в сокращённом виде следующим образом:

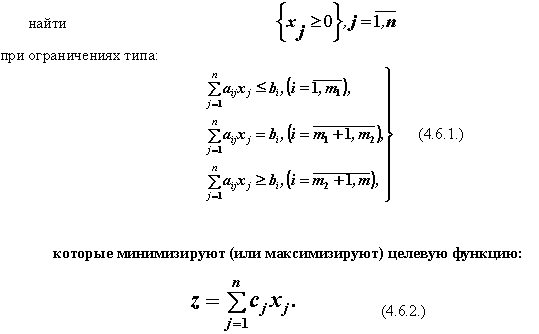
5.6.3. Геометрическая интерпретация задачи ЛП

Задача линейного программирования геометрически может быть проиллюстрирована следующим образом.

Пусть необходимо найти минимум целевой функции:

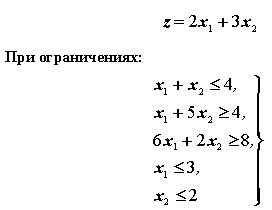
Переменные x₁ и x₂ должны быть неотрицательными.

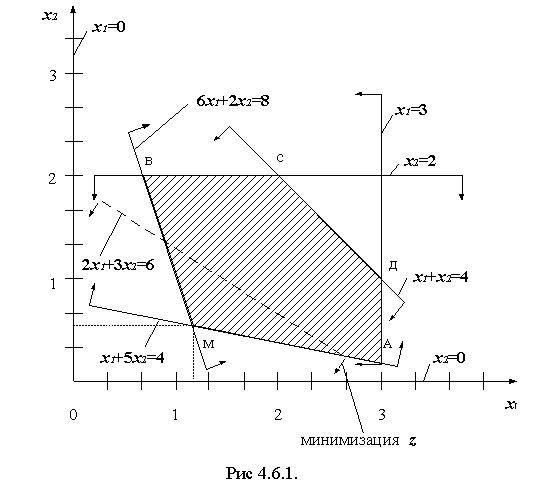
Поэтому множество точек, являющихся возможными (допустимыми) решениями, может находиться в первом квадранте (см. рис. 4.6.1.). Неравенства–ограничения изображены в виде полуплоскостей, границами которых являются прямые (графики функций), полученные из неравенств путём отбрасывания знаков >, <. Полуплоскости образуют выпуклый многоугольник (многоугольник решений – симплекс).

Линейная форма (линия уровня) для некоторого набора фиксированных значений переменной z представляет собой семейство параллельных прямых. Одна из них, которая пройдёт через вершину многоугольника “М”, ближайшую к началу координат и даст минимум z (для координат вершины).

Определив координаты точки М (8/7;4/7) получим:

z = 2× 8/7 + 3× 4/7 = 4

5.6.4. Основная идея методов решения задач ЛП

Графический способ решения (перемещение графика целевой функции по симплексу) приемлем только для двухмерных задач (задач на плоскости). Но геометрическое толкование задачи линейного программирования справедливо и для общего случая (m ограничений и n переменных). Каждое из соответствующих неравенству уравнений системы определяет некоторую гиперплоскость в n – мерном пространстве. Множество неотрицательных решений образует выпуклый многогранник в n – мерном пространстве. Линейная форма z -гиперплоскость, перемещая которую параллельно самой себе, будем получать множество точек пересечения её с выпуклым многогранником. Максимальное или минимальное значение линейной формы z достигается в точках, являющихся вершинами выпуклого многогранника.

В силу трудности решения задачи графическим способом в случае m ограничений и n>2 переменных применяют другие методы решения задачи ЛП. Наиболее распространённым и удобным является симплекс метод решения задачи ЛП.

Для решения задачи линейного программирования симплекс-методом применяется специальный аппарат формальных преобразований математической модели. Рассмотрим некоторые его положения. Пусть задана основная задача линейного программирования (см. (4.6.1.) и (4.6.2)). Введя в левую часть каждого неравенства добавочную переменную, преобразуем его в уравнение и перейдём к другой, стандартной форме записи:

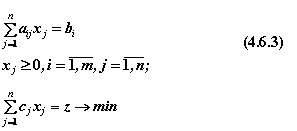
При этом значения b_i должны быть неотрицательными. В случае b_i < 0 обе части уравнения умножают на ”- 1”. Заметим, что при максимизации z задача сводится к стандартной путём замены: max z = - min (- z).

Систему (4.6.3) после несложных преобразований можно привести к виду:

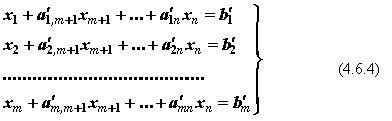
Здесь b_i ³ 0. Коэффициенты при переменных 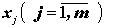< FONT> равны единице (+1). Данная система представлена в канонической форме записи. Если количество переменных превышает количество уравнений, то существует бесчисленное множество решений системы.

Пусть m < n. Разделим все переменные системы (4.6.4) на две части:

а) основные переменные, количество которых должно быть равно количеству линейно-независимых переменных (m);

б) неосновные переменные, количество которых будет равно n – m.

Назначим первые m переменных (x₁, x₂, …,x_m) в качестве основных. Тогда систему (4.6.4) можно решить относительно x₁, x₂, …,x_m, если определитель m-го порядка, составленный из коэффициентов при переменных x₁, x₂, …,x_m не равен нулю (Д ¹ 0).

Придавая неосновным (независимым) переменным произвольные числовые значения, получим некоторое решение данной системы, причём каждому набору значений независимых переменных будет соответствовать одно определённое решение системы.

Основные (зависимые, несвободные) переменные будем называть базисными, неосновные (независимые, свободные) – небазисными переменными.

Можно составить бесчисленное множество различных наборов значений независимых переменных. Из всех этих решений в линейном программировании нас будет интересовать так называемые допустимые базисные решения.

Допустимое базисное решение системы линейных уравнений при m < n – это такое решение, в котором неосновным (независимым, небазисным) переменным даны нулевые значения, а значения базисных переменных являются неотрицательными (решение на грани или вершине симплекса).

В теории линейного программирования доказывается, что если оптимальное решение задачи существует, то оно совпадает по крайней мере с одним из допустимых базисных решений.

Поиск и направленные переходы от одних допустимых базисных решений к другим с целью определения оптимального решения может быть выполнен численным методом. Один из них рассмотрим ниже.

Рассмотрим вычислительные и логические процедуры, обеспечивающие поиск решения задачи линейного программирования симплекс-методом. Процедуры поясняются в процессе решения конкретной задачи: найти совокупность значений, удовлетворяющих системе неравенств:

Таким образом, идея симплекс-метода преобразования модели заключается в таком интерактивном направленном переходе от одного допустимого базисного решения к другому, при котором последовательно улучшается значение линейной формы.

5.6.5.Симплекс-метод решения задач линейного программирования

Симплекс-метод является наиболее распространенным универсальным методом. Существует несколько вариантов этого метода, рассмотрим один из них.

Необходимо предварительно выполнить следущие этапы:

- привести математическую модель к каноническому виду;

- определить начальное допустимое базисное решение задачи;

Пример:

L=3x₁+2x₂®max

x₁-x₂£2,

2x₁+x₂£6,

x₁,x₂³0

Приведем заданную модель к каноническому виду, введя свободные переменные x₃ и x₄, превращающие неравенства в равенства. Переменные x₃ и x₄ входят в уравнение с коэффициентом единица и только один раз:

L=3x₁+2x₂®max

x₁-x₂+x₃=2,

2x₁+x₂+x₄=6,

x_j³0

где x₃, x₄ - дополнительные переменные, x₁, x₂ - свободные переменные, A₃ , A₄ - начальный базис, A₀ -вектор ограничений.

Составим симплекс - таблицу, соответствующую каноническому виду,:

Табл. 0						q
i	Csi	базис	A0	A1	A2	A3	A4
		A3			-1			2Ümin
		A4
	D		-3	-2
	Z
			Ýmin

Элементы строки D расчитываем по формулам:

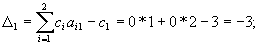
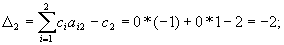
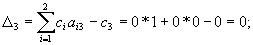
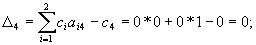
Для базисных переменных оценки всегда равны нулю.

Значение критерия для данного начального базиса будет равно нулю:

L=åc_ia_i0=0*2+0*6=0;

Так как имеются D_j<0 приступаем к улучшению плана.

Дата добавления: 2013-12-12