Определить пересечение двух прямых в 3-D пространстве

Примеры вычислительной геометрии.

Методы ВГ позволяют использовать аналитику для преобразования, хранения и воспроизведения различных геометрических объектов вычислительными методами.

Прямая.

1.Аналитическое уравнение прямой.

,

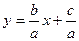
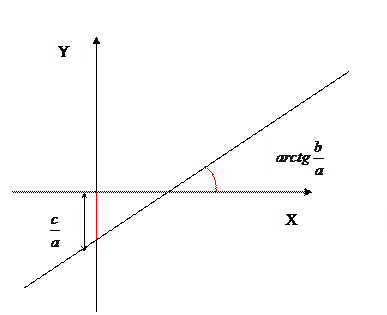
если а=0, тогда 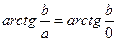, что непонятно и сложно для ЭВМ. Здесь нет закона, позволяющего построить каждую точку для получения полной КМД.

2.Параметрическое уравнение прямой.

Пусть прямая проходит через две точки P₁ и P₂. Каждая из этих точек в ДСК задаётся с помощью своего радиус- вектора 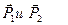.Прямая представляет из себя множество точек. Произвольная точка P, принадлежащая нашей прямой будет задаваться с помощью радиус-вектора .

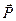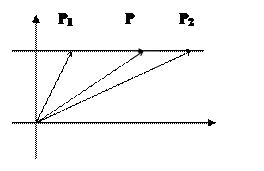
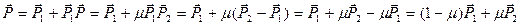
Здесь положение вектора 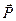для воспроизведения текущей точки определяется неким коэффициентом пропорциональности 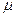, который показывает перемещение вектора 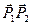.Видно, что при 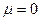попадаем в точку P₁ (вектор 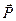совпадает с вектором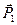), а при 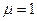попадаем в точку P₂

Т.о.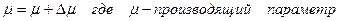

Используется линейное приращение, можно воспроизвести все точки прямой.

1-я прямая проходит через точки: M₁(1,1,1); M₂(2,3,4)

2-я прямая проходит через точки: N₁(1,2,3); N₂(-2,-3,-4)

Запишем параметрическое уравнение для каждой прямой:

:

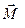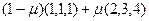
В декартовых координатах прямые:

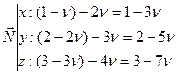
Условие пересечения 2-х прямых предполагает наличие одной общей точки. Приравниваем выражения для соответствующих координат:

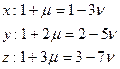
Решение сводится к нахождению 2-х линейно-независимых уравнений, их решению относительно неизвестных и проверке третьего (подстановкой). Выразим из 1-го уравнения 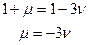Подставим полученное выражение в 3-е уравнение:

, соответственно .

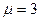Для проверки подставляем во 2-е уравнение:

1+6=2+5

Полученные параметры 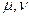подставим в уравнения и при условии равенства координат в обоих уравнениях получим точки пересечения:

-2(1,1,1)+3(2,3,4) = (4,7,10)

2(1,2,3)+(-1)(-2,-3,-4)= (4,7,10)

Прямые пересекаются.

Дата добавления: 2013-12-12