Основные сведения теории графов

Если граф G (рис.1) задается множеством Х точек или вершин x₁ , x₂ ,..., x_n и множеством А линий или ребер a₁ , a₂ ,..., a_m, соединяющих все или часть этих точек, то считают, что граф полностью задается парой (X, А).

Если ребра из множества А ориентированы, что показывается стрелкой, та они называются дугами (дуга от вершины x_i к вершине x_j обозначается а = (x_i, x_j)) и граф называется ориентированным графом (орграфом) (рис.1). Если ребра не имеют ориентации, то граф называется неориентированным гра­фом (неографом).

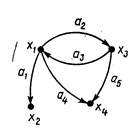
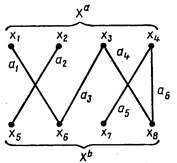
Рис.1. Ориентирован­ный граф Рис.2. Двудольный граф

Ребра а = (x_i, x_j), x_i ¹ x_j, имеющие общую концевую вершину, называ­ются смежными. Две вершины называются смежными, если существует хотя бы одно ребро, соединяющее эти вершины.

Ребро а = (x_i, x_j) инцидентно вершинам x_i, x_j и, наоборот, вершины x_i, x_j инциденты ребру а. Число ребер, инцидентных вершине xi, называется сте­пенью вершины. Графы, для которых сохраняется отношение инцидентности, называются изоморфными графами.

Если ребрам графа G сопоставляются числа, т. е. ребру (x_i, x_j) ставится в соответствие некоторое число с_ij, называемое весом ребра, то граф G называ­ется графом со взвешенными ребрами. Иногда веса приписываются вершинам, тогда граф называется графом со взвешенными вершинами. Если веса приписаны и ребрам и вершинам, то граф называется взвешенным графом.

Граф G = (X, А), у которого существует хотя бы одна пара вершин, сое­диняемых т ребрами (m > 1), называется мультиграфом. Ребра, связывающие одну и ту же пару вершин, называются кратными ребрами.

Граф G = (X, А) называют полным графом, если для любой пары вершин x_i и x_j во множестве Х существует по крайней мере одно ребро, связывающее их.

Граф G = (X, А) называется двудольным графом (биграфом), если множе­ство его вершин Х может быть разбито на такие два подмножества Х ^a и X ^b, что каждое ребро имеет один конец в подмножестве Х ^a, а другой — в подмножестве X ^b (рис.2).

Граф называется планарным графом, если его можно изобразить на плоскости так, что никакие два его ребра не пересекаются.

Плоский граф — граф, изображенный на плоскости без пересечения ребер.

Пространственный граф — граф, изображенный в трехмерном простран­стве.

Подграфом графа G = (X, А) называется граф G' = (X', А'), для которого А' с А и X' с X.

Суграфом графа G = (X, А) называется граф G' = (X, А'), для которого А' с А.

Пусть G = (X, А) — неориентированный граф без петель (ребер (x_i, x_i)) и кратных ребер. Маршрутом s в графе G называется последовательность ребер, в которой пары соседних ребер a_i, a_i+1 (i = 1,2,..., n -1) — смежные (n — длина маршрута). Маршрут s, в котором нет повторяющихся ребер, — цепь. Если в некоторой цепи совпадают начальная и конечная вершины, то такая цепь называется циклом с. Цикл будет простым, если у него нет повторяющихся вершин, и сложным в противном случае. Цикл с_э, в котором содержатся все ребра графа, называется эйлеровым. Цикл с_г, проходящий через каждую верши­ну графа G по одному разу, называется гамильтоновым.

Связный граф — граф, в котором две любые вершины можно соединить цепью. Связный граф без циклов называется деревом Т. Множество деревьев графа G называется лесом. В дереве любые две вершины связаны единственной цепью.

Дата добавления: 2013-12-12