Определение монтажного пространства

Матричные эквиваленты для алгебраического задания графов

Для алгебраического задания графов и их обработки на ЭВМ ис­пользуются различные матричные эквиваленты.

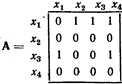
Матрицей смежности А = [а_ij]_{n x n} (n — порядок матрицы; п x п— размер матрицы) орграфа G называется матрица, у которой: а_ij = т, если в G существует т дуг (x_i, x_j); а_ij = 0, если в G нет дуги (x_i, x_j), n — число вершин.

Матрица смежности для графа, показанного на рис.1, имеет вид

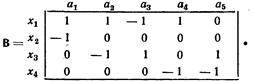
Для неографов а_ij равно числу кратных ребер между вершинами x_i и x_j, а матрица А симметрична. Матрицей инциденций B = [ b_ij ] _{n x m} (n x т — размер матрицы) для орграфа называется матрица, у ко­торой: b_ij = 1, если x_i является начальной вершиной дуги a_j; b_ij = -1, если x_i является конечной вершиной дуги а_j; b_ij = 0, если x_i не является вершиной дуги a_j или a_j является петлей; п — число вершин, т — число дуг в графе G.

Матрица инциденций для графа, показанного на рис.1, будет

Для неографа b_ij = 1, если вершина x_i инцидентна ребру а_j и b_ij = 0 в противном случае.

Для коммутационно-монтажного проектирования большое значе­ние имеют метрические свойства графов. Расстоянием d(x_i, х_j) между вершинами x_i, х_j ä Х графа G = (Х, А) называется длина кратчайшей цепи, соединяющей эти вершины. Под длиной цепи понимается число входящих в нее ребер. Функцию расстояния графа G удобно задавать матрицей расстояния D = [ d_tf ]_n´n,где

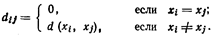
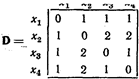
Для графа, показанного на рис.1, матрица D имеет вид

Для графа, рассматриваемого в системе координат XY, функция расстояний между вершинами x_i и х_j может быть определена следующими способами:

1. В евклидовой метрике – как расстояние между двумя точками на плоскости

.

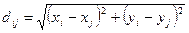2. В ортогональной (линейной) метрике (Манхетиново расстояние)

.

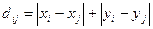3. В нелинейной метрике

,

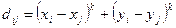где k = 2, 3, ….

Поскольку матрицыА, В, D в реальных задачах конструкторского проектирования сильно разрежены, т. е. в них относительно мало не­нулевых элементов, то хранить информацию в матричной форме не­эффективно. В этом случае переходят к списковым формам представ­ления матриц. Каждая из таких матриц полностью определяет граф.

Примечание. При решении задач конструкторского проектирования часто используются другого вида матрицы, которые будут описаны при рас­смотрении конкретных алгоритмов.

10.4. Графотеоретические модели монтажного пространства и коммута­ционных схем.

При коммутационно-монтажном проек­тировании (см[2,3]) необходимо оптимальное размещение конструктивных эле­ментов в соответствии с коммутационной схемой их соединения в не­котором монтажном пространстве с учетом заданной конструктивной базы и в соответствии с технологией изготовления межсоединений, а также трассировка соединений.

Монтажное пространство — метрическое пространство, в кото­ром размещаются элементы какого-либо узла, и осуществляется их электрическое соединение. Различают регулярные и нерегулярные монтажные пространства.

Регулярное монтажное пространство имеет прямоугольную фор­му, и одинаковые по размерам элементы располагаются с постоянным шагом по вертикали и горизонтали (например, печатная плата ТЭЗа, показанная на рис.3).

Нерегулярное монтажное пространство характеризуется тем, что элементы имеют разные размеры и форму и не имеют точно определен­ных посадочных мест (например, подложка ИС).

Математической моделью монтажного пространства является не­ориентированный взвешенный связный граф G = (X, А), в котором множество вершин соответствует посадочным местам в координатах XY, а множество ребер — связям между вершинами на координатной сетке. Вес ребер определяется в соответствии с выбранной метрикой монтажного пространства.

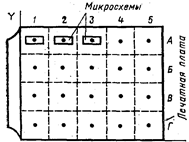
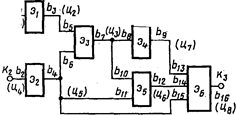
Рис. 3. Печатная плата ТЭЗа Рис. 4. Коммутационная схема

Граф G является полным графом и отра­жает все возможные варианты расположения конструктивных эле­ментов в данном монтажном пространстве и расстояния между ними. Выбор метрики определяется технологией изготовления межсоеди­нений, например для проводного монтажа используется евклидова метрика, для печатного — ортогональная.

На рис.4 приведена коммутационная схема соединений кон­структивных элементов э_i для некоторого узла, где k_j соответствуют внешним выводам схемы, a b_q — выводам конструктивных элемен­тов.

Дата добавления: 2013-12-12