Теорема сложения скоростей

Дифференцирование вектора в подвижных координатах (Формула Бура)

Пусть вектор 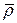представлен в подвижной системы координат в виде (рис.1.8):

.

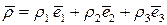Возьмём производную вектора 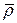по времени, учитывая, что орты подвижной системы координат изменяются по направлению:

.

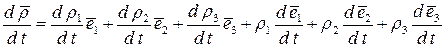Первые три слагаемые этой формулы дают нам относительную производную, обозначаемую как:

.

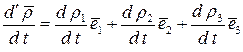Производная от единичного вектора — т. е. скорость конца этого вектора равна

.

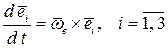Учитывая данное равенство, последние три слагаемых можно преобразовать следующим образом

.

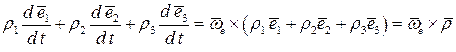Окончательно производная вектора 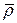по 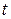будет записываться соотношением:

,

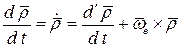где: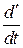— относительная (локальная) производная, в которой дифференцируются только координаты; 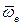— вектор угловой скорости подвижной системы координат.

Данная формула называется формулой Бура.

Абсолютная скорость точки при составном движении равна геометрической сумме переносной и относительной скоростей.

Пусть тело, с которой связана подвижная система координат, совершает произвольное движение относительно неподвижной системы координат. Это движение может быть рассмотрено как поступательное движение вместе с началом подвижной системой координат и сферическое относительно этого начала. Из векторного треугольника 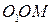получаем

.

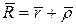Вычислив проекции этого векторного равенства на оси неподвижной системы координат, получим уравнения движения точки М.

Относительное движение будет характеризоваться координатами точки в подвижной системе координат:

.

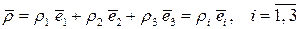Вычисляя производную вектора 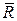по времени с помощью формулы Бура, получим:

.

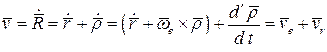Сумма слагаемых, стоящих в скобке, даёт скорость точки твёрдого тела, с которым "сцеплена" подвижная система координат, совпадающей с исследуемой точкой в данный момент времени. Эту скорость называют переносной

.

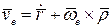Относительная производная даёт относительную скорость

.

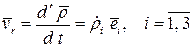Дата добавления: 2013-12-12