Теорема об ускорениях точек плоской фигуры

Примеры определения МЦС.

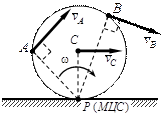При качении колеса радиуса r по шероховатой поверхности без проскальзывания, МЦС находится в точке касания колеса с неподвижной поверхностью

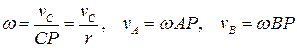
Если скорости двух точек плоской фигуры параллельны, но не равны друг другу, то (см. рис.1.14 а, в)

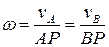
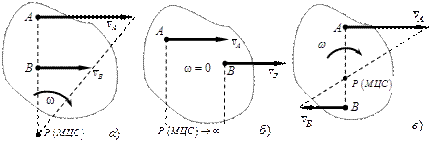
Рис. 1. 14. Скорости точек в плоском движении твердого тела

В случае равенства параллельных скоростей (см. рис.1.14 б) МЦС. находится в бесконечности.

Угловая скорость фигуры при этом равна нулю. Скорости всех точек равны. Говорят, что фигура совершает в рассматриваемый момент времени мгновенно поступательное движение, которое отличается от поступательного движения тем, что ускорения различных точек при этом не обязательно равны:

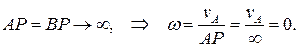
Если скорости двух точек антипараллельны, то (см. рис.1.14 в)

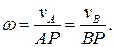
Ускорение произвольной точки твёрдого тела, участвующего в плоском движении, можно найти как геометрическую сумму ускорения полюса и ускорения данной точки во вращательном движении вокруг полюса.

Для доказательства этого положения используем теорему сложения ускорений течки в составном движении. Примем за полюс точку 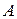. Подвижную систему координат будем перемещать поступательно вместе с полюсом (рис.1.15 а). Тогда относительным движением будет вращение вокруг полюса. Известно, что кориолисово ускорение в случае переносного поступательного движения равно нулю, поэтому

.

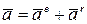Т.к. в поступательном движении ускорения всех точек одинаковы и равны ускорению полюса, имеем.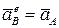

Ускорение точки при движении по окружности удобно представить в виде суммы центростремительной и вращательной составляющих:

.

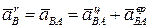Следовательно

.

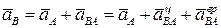Направления составляющих ускорения 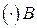показаны на рис.1.15 а.

Нормальная (центростремительная) составляющая относительного ускорения определяется формулой

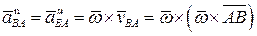
Величина его равна 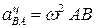Вектор 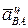направлен вдоль отрезка АВ к полюсу А (центром вращения 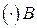вокруг 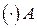является).

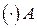Рис. 1. 15. Теорема о сложении ускорений (а) ее следствия (б)

Касательная (вращательная) составляющая относительного ускорения определяется формулой

.

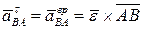Модуль этого ускорения находится через угловое ускорение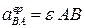. Вектор 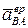направлен перпендикулярно к АВ в сторону углового ускорения (в сторону угловой скорости, если движение ускоренное и в противоположную сторону вращения, если движение замедленное).

Величина полного относительного ускорения определяется по теореме Пифагора:

.

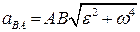Вектор относительного ускорения любой точки плоской фигуры отклонён от прямой, соединяющей рассматриваемую точку с полюсом на угол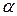, определяемый формулой

.

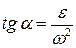На рис.1.15 б показано, что этот угол одинаков для всех точек тела.

Следствие из теоремы об ускорениях.

Концы векторов ускорений точек прямолинейного отрезка на плоской фигуре лежат на одной прямой и делят её на части, пропорциональные расстояниям между точками.

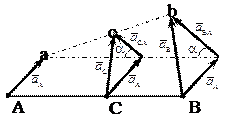Доказательство этого утверждения следует из рисунка:

.

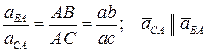Методы определения ускорений точек тела при плоском его движении идентичны соответствующим методам определения скоростей.

Дата добавления: 2013-12-12