
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сложение и разложение сил. Проекция силы на ось и на плоскость
|
|
|
|
СИСТЕМА СХОДЯЩИХСЯ СИЛ
Аксиома связей
Аксиома затвердевания.
Существенные сведения о равновесии деформируемых тел можно получить, воспользовавшись принципом отвердевания: если деформируемое тело находится в равновесии, то замена его или отдельных его частей соответствующими абсолютно твердыми телами не изменяет первоначального состояния равновесия. То есть условия равновесия абсолютно твердого тела являются необходимыми, но не достаточными для равновесия деформируемого тела.
Тела, равновесие которых изучается, в большинстве случаев контактируют с другими окружающими телами, ограничивающими свободу данного тела. Тела, ограничивающие свободу данного тела, являются по отношению к нему связями. Воздействия связей на тело называются реакциями связей. Мысленно отбросив все связи и заменив их воздействие реакциями, получим свободное тело, на которое действуют как приложенные (активные) так и реактивные силы (реакции связей). Этот прием имеет название принципа освобождаемости от связей.
Ниже на рис.2.6 – 2.10 представлены примеры связей и их реакций

Рис.2.6. Натянутые гибкие нити (а) и стержни (б)

Рис. 2.7 Идеально гладкая (а) и шероховатая (б) поверхности (контакт по поверхности)

Рис. 2.8 Неподвижная цилиндрическая шарнирная опора
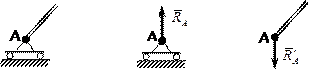
Рис. 2.9 Подвижная цилиндрическая шарнирная опора (опора на каток)

Рис. 2.10 Жесткая заделка
В соответствии с аксиомой сложения сил, две силы, приложенные к одной точке можно заменить одной — равнодействующей, которая находится по правилу параллелограмма или по правилу треугольника. Легко обобщить это правило на тот случай, когда к одной точке приложено более двух сил. Для нахождения их равнодействующей необходимо из конца первого вектора провести второй вектор и т. д. Поясним это на рис.2.11.
|
|
|

Рис.2.11 Равнодействующая сходящейсясистемы сил
Полученный многоугольник называется силовым, замыкающая сторона которого — вектор 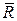 , определяет вектор равнодействующей, направлен из начала первого вектора силы в конец последнего вектора силы.
, определяет вектор равнодействующей, направлен из начала первого вектора силы в конец последнего вектора силы.
Решение задачи об определении суммы нескольких векторов (вектора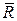 ) является единственным и не зависит от того, в каком порядке складываются слагаемые векторы.
) является единственным и не зависит от того, в каком порядке складываются слагаемые векторы.

Рис.2.12 Разложение силы на составляющие
Противоположный по смыслу алгоритм — разложение векторов, не имеет единственного решения, до тех пор, пока не заданы сами направления разложения сил.
Например, силу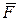 , расположенную в плоскости (рис.2.12), можно разложить по взаимно перпендикулярным осям
, расположенную в плоскости (рис.2.12), можно разложить по взаимно перпендикулярным осям  и
и , а можно и по любым другим
, а можно и по любым другим  и
и , При этом на оси
, При этом на оси  и
и , наложено всего одно условие — они не должны быть параллельны друг другу. Cилы
, наложено всего одно условие — они не должны быть параллельны друг другу. Cилы 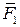 и
и 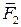 или
или 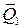 и
и 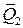 называются составляющими силы
называются составляющими силы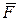 .
.

Рис.2.13 Проекции силы на плоскости
Рассмотрим понятие проекции силы на ось. Проекцией силы на заданную ось, например , называется скалярное произведение вектора силы
, называется скалярное произведение вектора силы 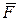 на единичный вектор
на единичный вектор , характеризующий положительное направление оси, т. е.
, характеризующий положительное направление оси, т. е.

Угол 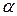 находится между положительным направлением оси
находится между положительным направлением оси  и направлением вектора силы
и направлением вектора силы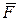 . В том случае, когда
. В том случае, когда  проекция
проекция  , т. к.
, т. к.  . Модуль этой проекции удобно вычислять через угол
. Модуль этой проекции удобно вычислять через угол  . В соответствии с определением проекции силы
. В соответствии с определением проекции силы 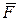 и скалярного произведения векторов можно записать
и скалярного произведения векторов можно записать
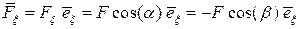
Вернемся к вопросу о разложении силы и рассмотрим эту процедуру в пространственном случае. Часто встречаются два варианта разложения: в первом случае (рис.2.13 а) ориентация вектора в пространстве задана двумя углами 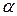 — между осью
— между осью 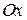 и направлением составляющей силы
и направлением составляющей силы 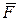 , лежащей в плоскости
, лежащей в плоскости  . и углом
. и углом 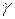 — между вектором
— между вектором 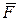 и его составляющей вдоль оси
и его составляющей вдоль оси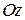 ; во втором случае (рис.2.13 б) положение вектора
; во втором случае (рис.2.13 б) положение вектора 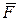 определяется тремя углами между направлением вектора
определяется тремя углами между направлением вектора 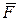 и положительными направлениями соответствующих осей:
и положительными направлениями соответствующих осей:  .
.
|
|
|

Рис.2.13 Проекции силы впространстве
Вначале разложим вектор 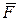 по двум направлениям
по двум направлениям 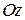 и
и 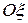 . Ось
. Ось 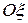 расположена в плоскости, проходящей через вектор силы
расположена в плоскости, проходящей через вектор силы 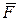 и ось Oz:
и ось Oz:

Вектор 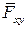 раскладывается по горизонтальным осям
раскладывается по горизонтальным осям 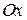 и
и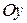 .
.

| Окончательно: | 
|
Последняя формула будет справедлива и при втором способе задания ориентации вектора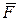 . В этом случае известны углы между вектором
. В этом случае известны углы между вектором 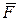 и направлением осей
и направлением осей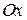 ;
; 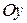 и
и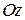 :
: . По определению проекции силы на ось имеем
. По определению проекции силы на ось имеем

Введённые понятия позволяют перейти к условиям равновесия системы сходящихся сил.
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 3273; Нарушение авторских прав?; Мы поможем в написании вашей работы!