Момент силы относительно точки на плоскости

ТЕОРИЯ МОМЕНТОВ. ТЕОРИЯ ПАР СИЛ.

Сходящаяся система сил. Условия равновесия систем сходящихся сил.

Сходящейся называют такую систему сил, линии действия которых пересекаются (сходятся) в одной точке.

Перенося силы вдоль линий их действия можно собрать сходящуюся систему в одной точке — точке пересечения линий действия сил. Далее, находим равнодействующую такой системы сил. Она равна векторной сумме этих сил. Система сходящихся сил будет уравновешенной (эквивалентной нулю) в том случае, когда ее равнодействующая равна нулю, т. е. уравнение 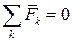является необходимым и достаточным условием равновесия системы сходящихся сил.

В плоском случае векторное условие равновесия эквивалентно двум скалярным уравнениям, которые мы получим, взяв проекции векторного равенства на оси, лежащие в плоскости действия сил:

,

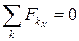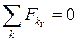
В трехмерном случае к этим уравнениям добавится еще одно независимое уравнение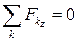

Следует подчеркнуть независимость этого числа (2 — в плоском и 3 — в пространственном случаях) уравнений. Можно составить сколько угодно подобных уравнений, выбрав в качестве осей какие угодно линии, но использовать можно только два (или три — в пространственном случае) любые из них.

Если к телу, имеющему закрепленную точку, приложить силу, то она будет оказывать вращательное действие.

Меру вращательного действия силы называют моментом силы. Алгебраический момент силы относительно данной точки равен произведению модуля силы на кратчайшее расстояние от данной точки до линии действия силы. Это расстояние называют плечом силы.

Вращательное действие силы принято считать положительным, если оно направлено против часовой стрелки. Момент силы зависит от: модуля силы; плеча силы; положения плоскости поворота; направления поворота в этой плоскости и выражается формулой (рис.2.14)

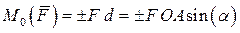
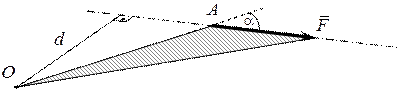
Рис.2.14 Алгебраический момент силы относительно точки на плоскости

Очевидно, что момент силы не меняется при переносе ее вдоль линии действия.

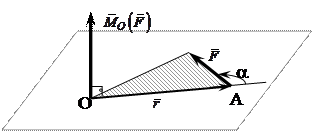
Рис.2.15 Векторное представление момента силы относительно точки

Алгебраический момент силы равен нулю только в том случае, когда равна нулю сила или линия ее действия проходит через точку, относительно которой определяется момент.

Дата добавления: 2013-12-12