Основная теорема статики

Лемма о параллельном переносе силы

ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ

Силу можно переносить параллельно самой себе в любую точку твёрдого тела, добавляя при этом пару сил с моментом, равным моменту переносимой силы относительно новой точки приложения силы.

Доказательство: Пусть на тело действует сила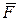, приложенная к некоторой точке А тела. В качестве центра приведения выберем произвольную точку 0 и приложим к ней уравновешенную систему двух сил {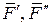}, линии действия которых параллельны силе.

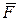Рис.2.19 Лемма Пуансо

Каждую из этих сил возьмём равной по величине исходной силе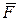. Очевидно, что полученная система сил эквивалентна исходной, причём силы 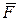и 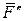образуют пару сил с моментом

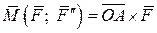
Метод приведения силы, рассмотренный в лемме, был предложен французским математиком и механиком Луи Пуансо (1777 — 1859) и называется методом Пуансо.

Произвольную систему сил, действующих на твёрдое тело, можно, в общем случае, привести к силе и паре сил.

Пусть на тело действуют 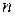сил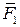, ,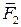… 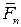произвольно расположенные в пространстве. Выберем произвольный центр приведения в теле. Пользуясь доказанной выше леммой, приведём каждую из сил к выбранному центру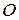. Получим систему сходящихся сил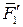, ,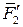… 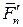и систему пар (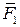;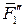), (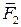;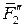),… (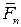;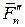). Система сходящихся сил, как известно, эквивалентна векторной сумме

,

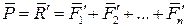а систему пар сил можно заменить эквивалентной парой с моментом, равным геометрической сумме моментов слагаемых пар

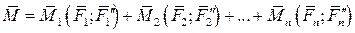или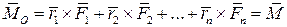

Вектор 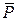для исходной системы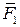, , 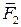…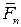не является равнодействующей и называется главным вектором исходной системы. Вектор 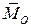называется главным моментом. Таким образом, исходная система заменена силой 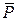и парой сил:

,

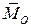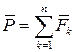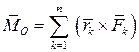
Дата добавления: 2013-12-12