Резонанс

Исследование вынужденных колебаний

Для дальнейшего исследования вынужденных колебаний, с целью упрощения преобразований, можно, не нарушая общности, принять нулевые начальные условия:

.

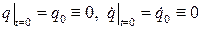Уравнение вынужденных колебаний в этом случае примет вид

,

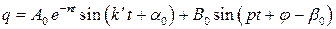где

,

.

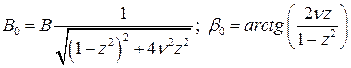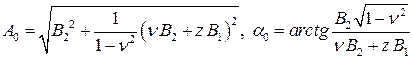Явление, возникающее при совпадении частот вынужденных и свободных колебаний механической системы, называется резонансом. В этом случае значение коэффициента расстройки 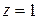. Уравнение движения, сдвиг фазы и амплитуда вынужденных колебаний определяются равенством

,

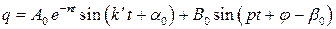где .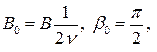

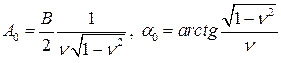Ошибка! Закладка не определена.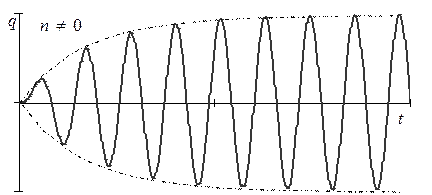

Рис. 3. 15 Резонансные колебания при наличии сопротивления.

Здесь, при наличии сопротивления движению и любом значении коэффициента демпфирования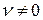, амплитуда вынужденных колебаний остается конечной величиной. График такого движения представлен на рис. 3. 15.

При отсутствии сопротивления 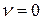уравнение колебаний теряет физический смысл, т.к. амплитуда вынужденных колебаний становится равной бесконечности. Для получения уравнения, описывающего явление резонанса при отсутствии сопротивления, разложим величину 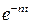в ряд по степеням 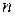и перейдем к пределу при,.

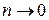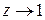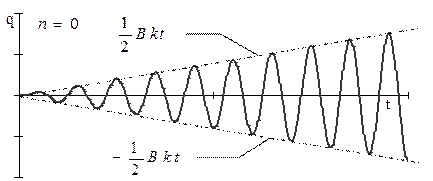
Рис. 3. 16 Резонансные колебания при отсутствии сопротивления.

Уравнение движения примет вид:

.

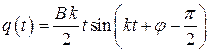Данное выражение показывает, что амплитуда вынужденных колебаний возрастает пропорционально времени. Частота и период вынужденных колебаний при резонансе и отсутствии сопротивления равны частоте и периоду свободных колебаний механической системы (см. рис. 3. 16).

Дата добавления: 2013-12-12