Дифференциальные уравнения поступательного движения твердого тела

ДИНАМИКА ТВЕРДОГО ТЕЛА

Частные случаи нахождения мгновенного центра скоростей

Следовательно, величины скоростей двух точек тела при плоско-параллельном движении относятся между собой как их расстояния от мгновенного центра скоростей.

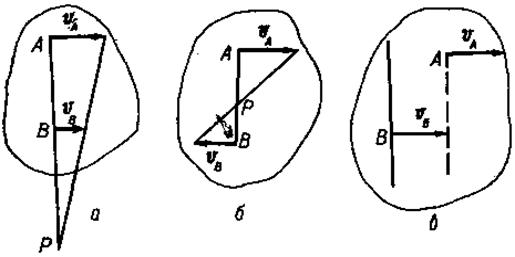
Если скорости двух точек плоской фигуры перпендикулярны к соединяющему их отрезку, то мгновенный центр скоростей находится в точке пересечения указанного отрезка с прямой, соединяющей концы векторов скоростей двух точек (рис. 74, а, б). В случае, когда скорости двух точек плоской фигу­ры равны и параллельны (рис. 74, в), то мгновенный центр скоростей удаляется на бесконеч­ность, т. е. движение мгновенно поступательное.

Пусть тело под действием приложенных к нему сил движется поступательно. Применяя теорему о движении центра масс (центра инерции), можно получить дифференциальные уравнения поступа­тельного движения тела. Действительно, по (111.65),

mω_c=R,

где m — масса тела;ω_c= r_c— ускорение его центра инерции, R — главный вектор внешних сил, приложенных к телу.

В проекциях на оси координат получим

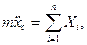
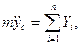
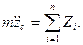
Интегрируя эти уравнения, можно определить координаты цент­ра инерции тела как функции времени. Постоянные интегрирования определяются из начальных условий движения (при t=t₀:

).

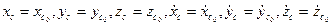Указанные уравнения можно также получить исходя из уравне­ний Лагранжа второго рода.

Обозначим координаты центра инерции твердого тела через х_c, у_c, z_c и примем их за обобщенные координаты:

q₁=x_c, q₂=y_c, q₃=z_c.

Поступательное движение тела полностью определяется движе­нием его центра инерции, а поэтому число степеней свободы тела равно трем (k =3) и уравнения Лагранжа второго рода в этом слу­чае будут иметь вид

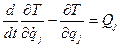(j=1,2,3).

Кинетическая энергия тела равна

и, следовательно,

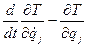(j=1,2,3).

соответственно равны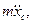

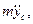
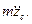
Далее, определяя

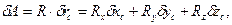
найдем обобщенные силы Q_j (j=1, 2, 3):

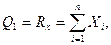
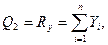
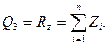
Составляя уравнения Лагранжа, получим уравнения (111.217).

Дата добавления: 2013-12-12