Погрешности дискретизации и восстановления

Dt 2Dt 3Dt 4Dt Рис. 3.6

x_д(t)

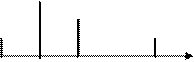0 Dt 2Dt 3Dt 4Dt t

- дискретизированный сигнал

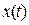- исходный сигнал.

- периодическая последовательность - импульсов

Разложим периодическую последовательность d-импульсов в ряд Фурье, как мы это делали выше:

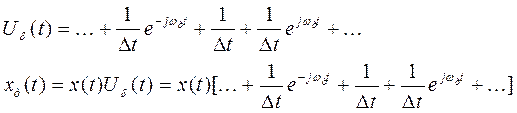
Найдём спектр дискретизированного сигнала.

(3.4)

Т.о. мы видим, что спектр дискретизированного сигнала содержит спектр исходного сигнала S _x (w), спектр исходного сигнала смещенный на величину частоты дискретизации вправо S _x (w - w_д), тот же спектр смещенный на величину частоты дискретизации влево S _x (w+ w_д), тот же спектр смещенный на величину 2 w_д и т.д.

Спектр исходного непрерывного сигнала.

S_x(w)

Рис.3.8

-w_g w_g w

Спектр дискретизированного сигнала: _·

S_д(w)

Рис.3.9

……….. …………

(-w_д - w_в) - w _д - w_в 0 w_в w_д (w_д + w_в) w

3.3. Спектр дискретизированного сигнала при дискретизации импульсами конечной длительности (сигнал амплитудно-импульсной модуляции или АИМ сигнал).

Очевидно, что реально мы располагаем не последовательностью дельта-импульсов, а последовательностью импульсов конечной длительности.

В результате процесса дискретизации мы получим не последовательность дельта-импульсов, амплитуда которых соответствует значению непрерывного сигнала в тактовые моменты времени, а последовательность реальных, например, прямоугольных импульсов, амплитуда которых соответствует значениям непрерывного сингнала в тактовые моменты времени.

Рассмотрим временные диаграммы:

x(t) аналоговый сигнал

t

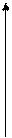U(t) периодическая последовательность импульсов

t

x_аим(t) сигнал АИМ

t

0 Dt 2Dt 3Dt 4Dt ……

Рис.3.10.

АИМ сигнал можно записать в виде:

U(t)-периодическая последовательность импульсов.

В квадратных скобках – ряд Фурье для последовательности импульсов конечной длительности.

Спектр АИМ сигнала,следовательно, похож на спектр дискретизированного сигнала при дискретизации дельта -импульсами, но амплитуда составляющих спектра убывает с ростом номера гармоники: (3.5)

Спектр АИМ сигнала в соответствии с формулой (3.5) принимает вид, показанный на рис.3.11.

_·

S_д(w)

-2 w_д - w _д - w_в 0 w_в w_д 2w_д w

Рис.3.11

3.4. Восстановление непрерывного сигнала из отсчётов.

В линию связи передаются импульсы-отсчёты, которые поступают на вход приёмника.

Для восстановления исходного непрерывного сигнала из импульсов-отсчётов надо эти импульсы подать на вход идеального фильтра низких частот (ИФНЧ), который имеет следующие характеристики.

Амплитудно-частотная характеристика идеального ФНЧ (АЧХ ИФНЧ) имеет вид:

K(w)

K

- w_д 0 w_д w

Рис.3.12

Импульсная реакция ИФНЧ, т.е. реакция на дельта-импульс имеет вид:

g_ифнч (t)

Рис. 3.13

t

-3 Dt - 2Dt -Dt 0 Dt 2Dt 3Dt

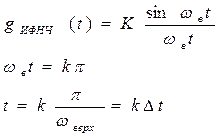(3.6)

Первая формула - это выражение для импульсной реакции ИФНЧ, вторая и третья формулы определяют моменты времени, для которых

g _ИФНЧ (t) обращается в ноль.

Cо спектральной точки зрения мы пропускаем дискретизированный сигнал, имеющий спектр в соответствии с рис.3.9 или 3.11, через ИФНЧ с АЧХ рис.3.12. Очевидно, что на выходе ИФНЧ получим спектр:

S(w)= K S_д(w) = K S_x(w) /Dt;

или для АИМ сигнала получим: S(w)= KS_д(w) = K a₀S_x(w) /2.

Таким образом, с точностью до постоянного множителя мы получили на выходе ИФНЧ спектр исходного сигнала x(t). С временной точки зрения мы получили исходный непрерывный сигнал x(t).

Дата добавления: 2013-12-12