
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свободные и затухающие колебания
|
|
|
|
Пружинный маятник
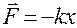
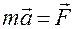
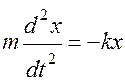
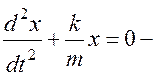 дифференциальное уравнение гармонических колебаний, его решение x = A Sin (ωt + φ0)
дифференциальное уравнение гармонических колебаний, его решение x = A Sin (ωt + φ0)
где 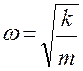
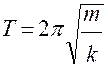
Свободные затухающие колебания – колебания, амплитуда которых с течением временем уменьшается из-за потерь энергии реальной колебательной системой.
Свободные колебания – колебания в колебательной системе, без внешнего воздействия.
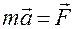

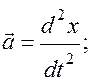
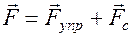
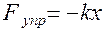
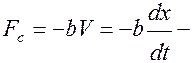 сила сопротивления,
сила сопротивления,
b - коэффициент сопротивления,
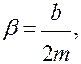
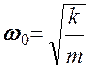
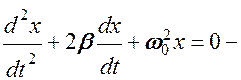 дифференциальное уравнение затухающих колебаний.
дифференциальное уравнение затухающих колебаний.
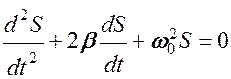 (*)
(*)
где S – изменяющаяся при колебаниях физическая величина.
β – коэффициент затухания.
ω0 – циклическая частота свободных незатухающих колебаний (т.е. при β = 0).
Решение этого уравнения
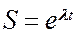 , (* *)
, (* *)
общее решение 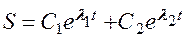 ,
,
где С1 и С2 – постоянные коэффициенты, зависящие от условий;
λ1 и λ2 – корни характеристического уравнения, получающегося из * подстановкой в него * *
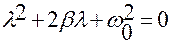
Если β < 0, то корни этого уравнения комплексные
λ1, 2 = - β ± 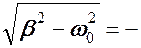 β ± iω
β ± iω
где 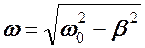
Общее решение:
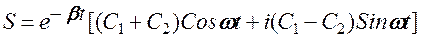
или на основании формулы Эйлера
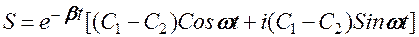
Вводя вместо С1 и С2 две новые постоянные А0 и φ0
А0 Sin φ0 = C1 + C2
i(C1 – C2) = A0 Cos φ0
и окончательно 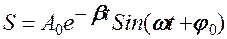
Постоянные А0 и φ0 зависят от начальных условий, т.е. от значений S и 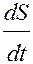 в начальный момент времени.
в начальный момент времени.

Затухающие колебания, строго говоря, не являются периодическими, т.к. максимальное значение колеблющейся величины S достигаемое в некоторый момент t1 в последующем никогда не повторяется
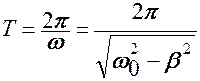 период (условный период) затухающих колебаний.
период (условный период) затухающих колебаний.
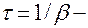 время релаксации (амплитуда колебаний уменьшается в e раз)
время релаксации (амплитуда колебаний уменьшается в e раз)
δ = 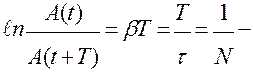 логарифмический декремент затухания.
логарифмический декремент затухания.
N – число колебаний, в течение которых амплитуда уменьшается в e раз
т.к. 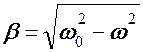 и
и 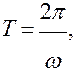 то
то
δ = βT = 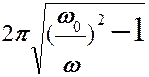 и
и
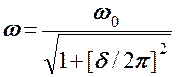
Добротность Q – величина, равная 2π, умноженная на отношение энергии W(t) колебательной системы в момент времени t к убыли этой энергии за один период
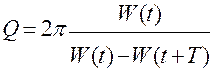
W(t) ~ A2 → 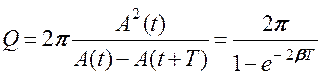
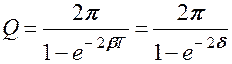
При малых значениях логарифмического декремента затухания
(δ << 1) 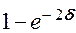 ≈ 2δ и
≈ 2δ и
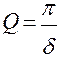
при этом ω ≈ ω0 → 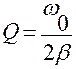
При β = ω0 T→ ∞ и процесс становится апериодическим (т.е. колебаний не возникает).
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 617; Нарушение авторских прав?; Мы поможем в написании вашей работы!