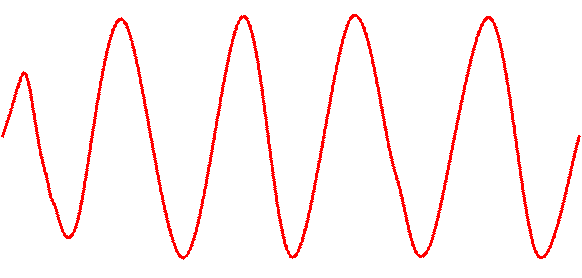
Вынужденные колебания осциллятора под действием синусоидальной силы

Дифференциальное уравнение вынужденных колебаний имеет вид

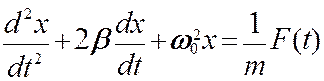
β и ω₀ имеют прежний смысл

Если F(t) – периодическая функция времени, то после приложения этой силы возникает переходный режим вынужденных колебаний, при которых осциллятор одновременно участвует в двух колебаниях:

S(t) = x₁(t) + x₂(t)

x₁(t) соответствует свободным затухающим колебаниям

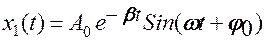
где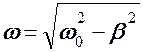

x₂(t) соответствует незатухающим периодическим колебаниям с частотой, равной частоте вынуждающей силы F(t).

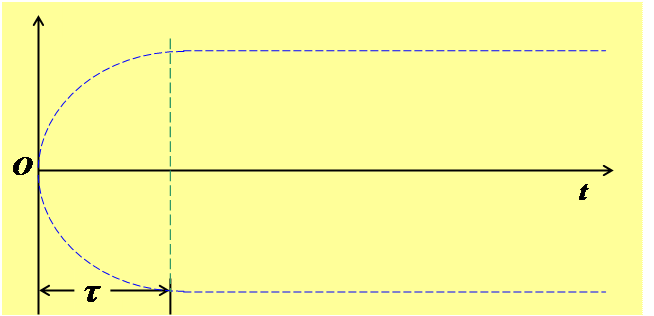
Амплитудное значение x₁(t), равное A₀e^-βt, быстро уменьшается после начала вынужденных колебаний: и за время 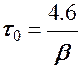амплитуда x₁(t) уменьшается в 100 раз. Следовательно, через некоторое время τ после начала колебаний (τ ~ τ₀) свободные колебания практически прекращаются:

x(t) ≈ x₂(t)

Наступает состояние установления вынужденных колебаний, происходящих с частотой возмущающей силы. Если учесть, что при малых затуханиях Q ≈ 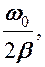то время установления τ можно оценить по формуле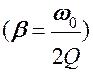

τ ~ 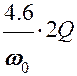~ 10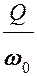

т.е. чем больше добротность осциллятора, тем больше время его установления τ.

Пусть

F(t) = F₀ Cos Ωt,

где F₀ – амплитуда вынуждающей силы.

Установившиеся вынужденные колебания будут также гармоническими с той же частотой Ω, т.е.

x(t) = A Cos(Ωt + φ₀)

Подставив это в дифференциальное уравнение вынужденных колебаний, можно получить:

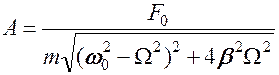
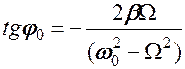
При Ω = 0 получим φ₀(0) = 0

и А(0) = А₀ = 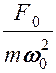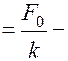статическое смещение из положения равновесия под действием постоянной силы F₀.

При Ω → ∞ получим A(Ω) → 0 и tg φ₀ → 0, а φ₀ → - Ω.

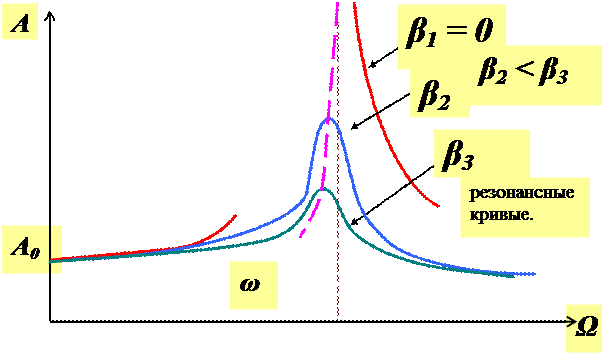
График зависимости A(Ω) и φ₀(Ω) показан на рисунках

O

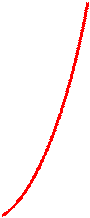
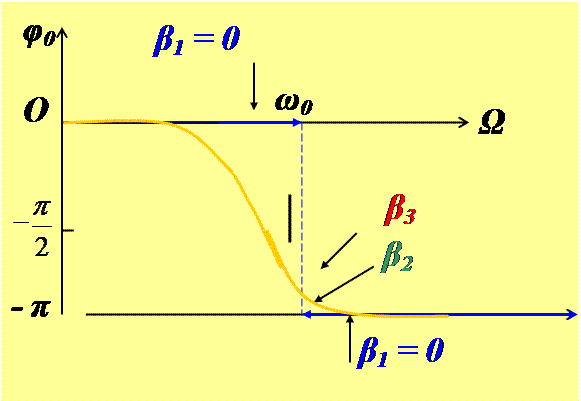
Частоту установившихся вынужденных колебаний Ω_р, при которой амплитуда А достигает наибольшего значения (резонансную частоту вынужденных колебаний), можно найти из условия минимума знаменателя в выражении для А.

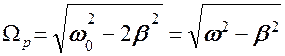
где ω – частота свободных затухающих колебаний

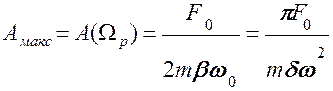
где δ = βТ = 2πβ/ω – логарифмический декремент затухания.

Дата добавления: 2013-12-12