Уравнение обобщающее закон кулона теорема Гаусса

Силовые линии поля

Линии касающиеся в каждой точке векторов Е, Н, Д, В получили название соответствующих силовых линий поля.

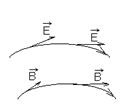
С помощью картинок силовых линий удобно изображать как направление поля так и величину соответствующей характеристики в данной области пространства (чем гуще силовые линии, чем больше силовых линий проходит через некоторую силовую площадку тем в данной области пространства больше величина соответствующего силового вектора (Е, Н, Д, В). Картинку силовых линий того или иного силового поля вектора А можно получить решив дифференциальной уравнение.

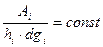
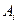- проекция вектора А (Е, Н, Д, В) на итую координату обобщённой криволинейной системы координат; 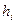- коэффициент Ламе; 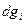- элемент соответствующей итой координаты.

Получим одно из основных соотношений электростатики с помощью которой просто рассчитать характеристики электростатического поля (ЭСП) созданного заряженными структурами сложной формы. Рассмотри некоторый заряд 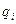из семейства точечных зарядов. Напряжённость поля в точке находящейся на расстоянии r от данного заряда может быть определено:

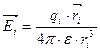
Если мы имеем семейство точечных зарядов то для нахождения ЭП созданного всем семейством удобно применить принцип суперпозиции (напряжённость ЭП в искомой точке пространства созданного всем семейством заряженных тел будет равен геометрической суме напряжённости полей созданной в данной точке пространства всеми заряженными подсистемами данной заряженной системы)

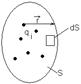
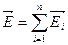
Окружим данную систему заряженных тел замкнутой поверхностью S. Выделим на данной поверхности S бесконечно малый элемент dS и определим поток (электрический поток) вектора индукции ЭП через данный элемент dS причём данное поле создаётся одним из итых зарядов семейства заряженных тел.

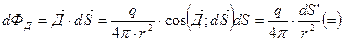
q – суммарный заряд находящийся в нутрии данной поверхности; 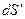- проекция площадки dS на плоскость перпендикулярную вектору 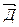; 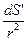=dΩ - элемент телесного угла опирающегося на элементарную площадку dS или элемент телесного угла под которым видна площадка dS из той точки в которой находится заряд. Отсюда выражение для элементарного потока:

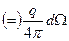
Определим поток через всю замкнутую поверхность в нутрии которой находится семейство точечных зарядов. 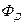равен сумме элементарных потоков через каждую элементарную площадку. Суммирование сводится к интегрированию по всей замкнутой поверхности S.

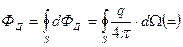
Из стереометрии известно, что телесный угол опирающийся на замкнутую поверхность равен 4π

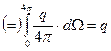
Таким образом мы доказали уравнение обобщающее закон кулона (теорема Гаусса)

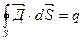- Интегральная форма

Поток вектора 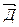через замкнутую поверхность S равен суммарному свободному заряду находящемуся внутри данной замкнутой поверхности.

Представленное выражение является записью теоремы Гаусса в интегральной форме для некоторой макро области пространства. Получим это же выражение в дифференциальной форме для некоторой точки пространства. Предполагаем что заряд в нутрии некоторой замкнутой поверхности S распространяется непрерывно по некоторому объему V с некоторой объёмной плотностью ρ. Суммарный заряд Q находящийся в нутрии данной замкнутой поверхности:

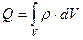
То уравнение Гаусса

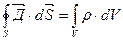
Используя известное соотношение векторного анализа теорему Остроградского Гаусса

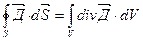
Уравнение обобщающее закон Кулона переписывается

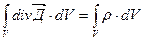
Это равенство может быть справедливо тогда когда

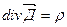-уравнение обобщающее закон кулона

в дифференциальной форме.

Дивергенция вектора электрического смещения равна объёмной плотности свободного заряда.

Дата добавления: 2013-12-12