Гармонический осциллятор

Механические гармонические колебания

Если материальная точка с массой m совершает гармоническое колебание вдоль оси x, то её координата относительно оси х определяется в соответствии с законом (1), а скорость и ускорение в соответствии с законами (2) и (3).

Сила действующая на материальную точку может быть определена:

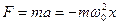
Знак минус говорит о том, что возвращающая сила за счёт сообщённой энергии направлена в сторону перемещения материальной точки. Как видно из данного выражения сила зависит от координат, что характерно для упругих сил, то возвращающею силу называют квазиупругой и она консервативна.

Зная закон изменения скорости и возвращающей силы можно определить полную механическую энергию свободного гармонического колебания в отсутствии диссипатии.

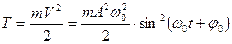
Потенциальную энергию можно определить исходя из общего соотношения определяющего взаимосвязь между потенциальной энергией и работой консервативных сил в поле которых тело обладает данной потенциальной энергией.

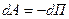
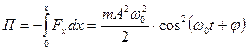
Тогда полная механическая энергия определяется:

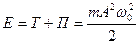
Как видно из полученного выражения как кинетическая так и потенциальная энергия меняются по гармоническому закону.

Таким образом в случае колебательного процесса как кинематические так и энергетические характеристики меняются по гармоническому закону.

Гармоническим осциллятором называется система колебания которая описывается как:

(*)

Рением данного дифференциального уравнения является выражение описывающее свободное незатухающее колебание но в природе таких системе существует так как любая колебательная система имеет потери, за счёт этого колебание становится затухающим. При малых затуханиях существует системы которые можно определить как гармонические осцилляторы. Пример: пружинный физический, математический маятники и колебательный контур.

Рассмотрим пример гармонического осциллятора.

Пружинный маятник: Если некоторое тело массой m присоединить к невесомой пружине и дать первоначальный точек то за счёт энергии упругой деформации будет происходить колебание тела массой m на пружине.

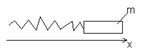Запишем уравнение второго закона Ньютона в проекции на ось х

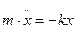
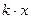- упругая сила под действием которой происходит движение тела массой m.

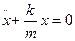
Последнее по форме совпадает с уравнением (*)

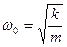
Период: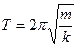

Физический маятник: Физическим маятником называется абсолютно твёрдое тело совершающее колебательное движение под действием силы тяжести вокруг горизонтальной оси не проходящей через центр тяжести данного тела

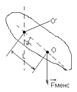
Для данного физического маятника можно записать основное уравнение динамики вращательного движения

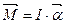
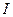- момент инерции тела;

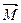- момент силы тяжести;

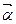- угловое ускорение.

В проекции на ось совпадающей с направлением угловой скорости

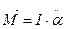
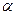- угол отношение прямой проходящей через ось вращения и центром тяжести отсчитанным от вершины.

Вращение происходит под действием тангенциальной составляющей силы по отношению к окружности радиусом 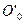составляющей силы тяжести. Поэтому данное уравнение:

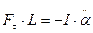
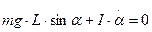
Учитывая что при малых углах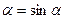

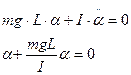
Таким образом получили дифференциальное уравнение типа (*) из которого можно определить угловую частоту физического маятника.

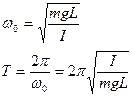
Приведённая длинна

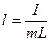
Если точку подвеса сместить на расстояние равное приведённой длине физического маятника то данный маятник будет совершать колебания с таким же периодом с каким совершаются колебания первоначально определённой оси повеса маятника.

Математический маятник: Называется тело m подвешенное на нить длинной L невесомую и не растяжимую. Которая совершает колебания под действием силы тяжести по этому математический маятник можно считать частным случаем физического маятника и соответственно получить его характеристики можно из уравнения физического маятника, но при этом считая тело массой m математической точкой и соответственно определить его момент инерции как:

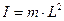
Тогда подставляя данное значение момента инерции в выражение для частоты физического маятника получаем что циклическая частота математического маятника:

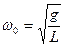
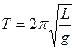
Приведённая длинна математического маятника будет равна самой длине математического маятника.

Дата добавления: 2013-12-12