
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение положений максимумов и минимумов методом зон Френеля
|
|
|
|
Таутохронность линзы и ее следствия
Дифракция Фраунгофера на щели
В случае дифракции Фраунгофера параметр b2/(Lλ) << 1 (19.1). Это значит, что если размер препятствия b ~ λ, то расстояние до экрана наблюдения L >> b.
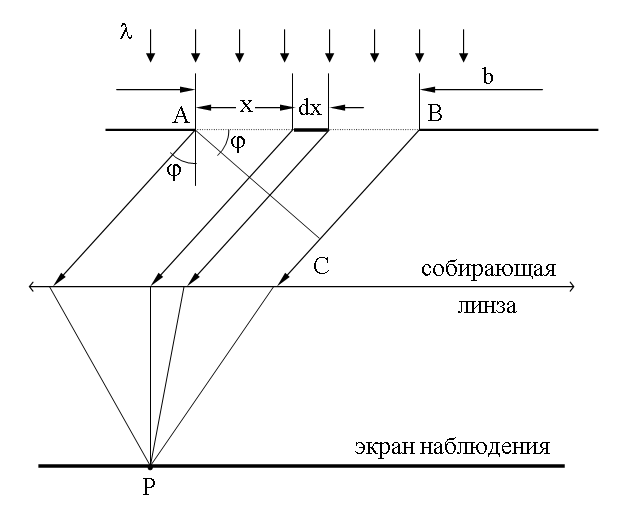
Пусть на длинную щель шириной b падает плоская монохроматическая волна с длиной λ.
Поместим между щелью и экраном наблюдения линзу так, чтобы экран наблюдателя находился в фокальной плоскости линзы. Линза позволяет наблюдать на экране дифракцию в параллельных лучах (L → ∞).
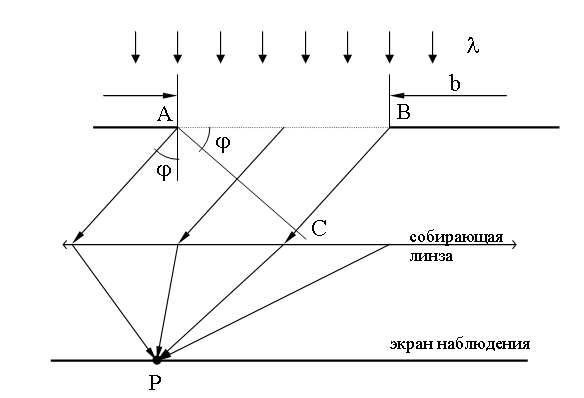
Собирающая линза обладает свойством, называемым таутохронностью: лучи, идущие от волновой поверхности AC до точки наблюдения P имеют одинаковую оптическую длину. Таким образом результат суперпозиции вторичных волн, который определяет амплитуду колебаний световой волны в точке P (см. 19.2), зависит от разности хода, набегающей в треугольнике ABC.
Для нахождения положений максимумов и минимумов интенсивности воспользуемся методом зон Френеля (19.3): разобьем сторону BC на отрезки длиной λ/2.
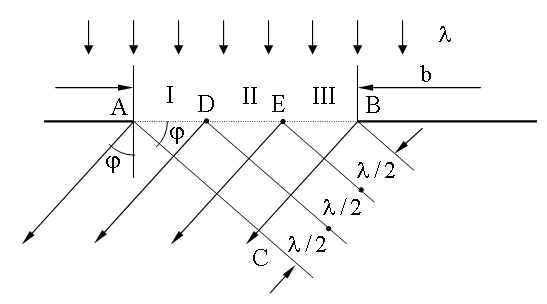
Из концов этих отрезков проведем линии, параллельные фронту вторичной плоской волны, идущей под углом φ. Эти линии разобьют AB - фронт первичной плоской волны на зоны Френеля. На рисунке их изображено три: AD, DE и EB. Число зон Френеля k зависит от λ и длины отрезка BC = b Sinφ. Если k целое, то
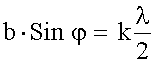 .
.
При четном числе зон Френеля k = 2m, где m = ±1, ±2... все зоны можно разбить на соседние пары, которые гасят друг друга (19.3). Следовательно условие минимума при дифракции Фраунгофера на щели имеет вид:

При нечетном k = 2m + 1 одна зона остается без пары и ее колебания не будут погашены, следовательно, условие максимума при дифракции Фраунгофера на щели будет иметь вид:
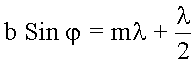 .
.
Обратим внимание, что условия формально противоположны условиям максимумов и минимумов (18.1.2.3) при интерференции от двух источников.
19.3.2.3. Зависимость интенсивности дифракционной картины от угла дифракции φ
Разобьем щель на полоски шириной dx и изобразим векторную диаграмму колебаний, посылаемых этими полосками в точку наблюдения P. При φ = 0 колебания от всех полосок будут иметь одинаковую фазу. Результирующее колебание в точке P получится в результате сложения сонаправленных бесконечно малых векторов. Векторная диаграмма (14.3) в этом случае будет иметь вид вектора длиной A0.
Для колебаний приходящих от щели в точку наблюдения P, расположенную под углом φ, векторная диаграмма имеет вид дуги окружности длиной A0.
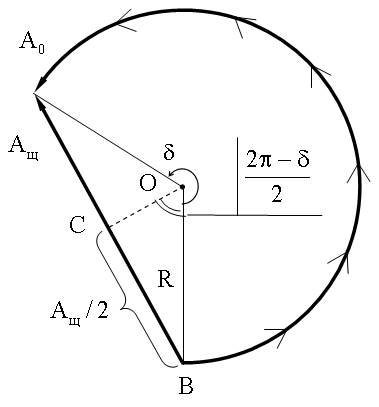
| Замыкающий эту дугу вектор Aщ является амплитудой результирующего колебания от щели при произвольном угле φ. Фазовый угол δ соответствует максимальной разности хода, равной Δ = b Sinφ. Так как
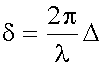 , см. (18.1.2.2), то , см. (18.1.2.2), то
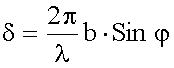 . .
|
Величину вектора Aщ найдем из геометрических соображений.
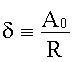 (по определению радианной меры угла).
(по определению радианной меры угла).
Из треугольника COB:
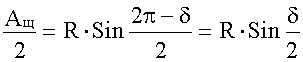 .
.
Исключив R получим:
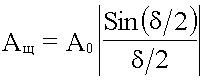 .
.
Интенсивность (16.5.4.) пропорциональна квадрату амплитуды, следовательно:
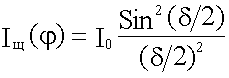 .
.
Учитывая связь δ с разностью хода Δ, получим связь интенсивности дифрагировавшего света с параметрами разбираемой задачи:
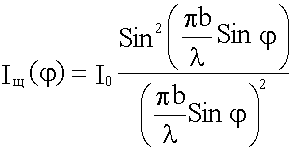 .
.
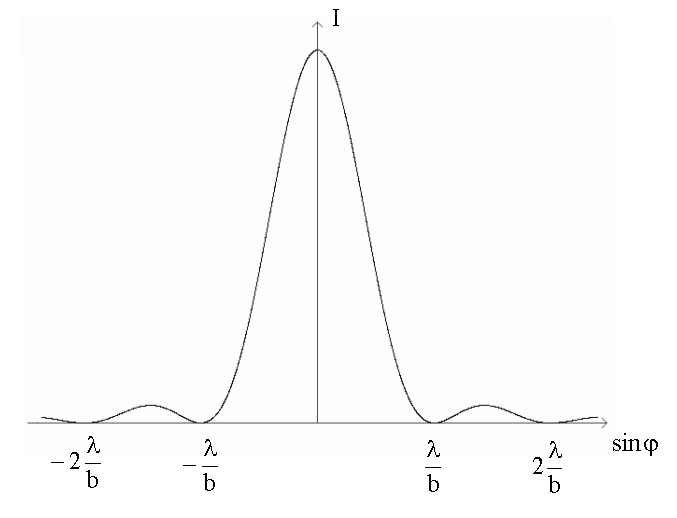
Здесь I0 - интенсивность при φ = 0.
График этой функции в осях I - Sinφ имеет следующий вид:
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 4283; Нарушение авторских прав?; Мы поможем в написании вашей работы!