Условие главного максимума для дифракционной решетки

Дифракционная решетка

- это совокупность большого числа одинаковых щелей, отстоящих друг от друга на одно и то же расстояние. Расстояние d между соответственными точками соседних щелей называют периодом решетки:

d = a + b.

Пусть на дифракционную решетку с числом щелей N падает по нормали параллельный пучок света (плоская волна, 15.1.7) с длиной волны λ. Между экраном и решеткой поместим собирающую линзу. Экран расположим в фокальной плоскости линзы. По принципу Гюйгенса-Френеля (19.2) для нахождения амплитуды результирующего колебания в какой-либо точке P экрана наблюдения надо найти результат интерференции всех вторичных волн, с учетом их фаз и амплитуд. Линза собирает в точке P все параллельные лучи, идущие от решетки под углом φ.

Каждая щель создает колебания с амплитудой зависящей от φ (19.3.2.3).

.

Разность хода лучей, идущих от соответственных точек соседних щелей найдем из треугольника ABC:

.

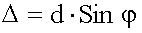При выполнении условия максимума (18.1.2.3)

,

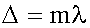таким образом, условие главного максимума для дифракционной решетки будет иметь следующий вид:

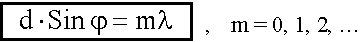
Целое число m называют порядком максимума. Колебания от соседних щелей при выполнении условия максимума в точку P будут приходить в одинаковой фазе. Результирующая амплитуда A_р, создаваемая в точке P решеткой будет в N раз больше амплитуды от одной щели:

.

Интенсивность света (16.5.4):

будет в N² раз больше, чем интенсивность I_щ, создаваемая одной щелью.

19.4.2. Зависимость интенсивности дифракционной картины решетки от угла дифракции φ

Амплитуда результирующего колебания от N щелей, A_p(φ), есть результат многолучевой интерференции (18.3). Таким образом:

.

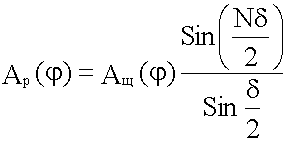Здесь δ - разность фаз колебаний, идущих в точку P от соответственных точек соседних щелей. Выразим δ через Δ (18.1.2.2), а Δ из треугольника ABC:

Подставив A_щ, полученную в (19.3.2.3), получим зависимость амплитуды результирующего колебания, создаваемого решеткой для угла φ:

.

Для интенсивности (16.5.4) получим:

.

Здесь I₀ - интенсивность, создаваемая одной щелью при φ = 0, первая дробь учитывает зависимость от интенсивности от φ одной щели, а вторая учитывает результат многолучевой интерференции N щелей.

При выполнении условия главного максимума d·Sinφ = mλ вторая дробь после раскрытия неопределенности по правилу Лопиталя дает N². Таким образом, интенсивность в максимуме, как и было показано в (19.4.1), в N² раз больше интенсивности, создаваемой одной щелью.

Дата добавления: 2013-12-12