Силы упругости

Эти силы возникают в твердом теле при его
деформировании (изменении его формы).
Простейшим видом деформации тела является его
растяжение или сжатие. Например, оно возникает
в тонком стержне, один конец которого

закреплен, а к другому приложена сила f
перпендикулярно основанию стержня. Упругое

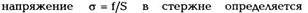
величиной силы f, отнесенной к площади
поперечного сечения стержня S. Это напряжение
одинаково вдоль всей длины стержня. Если
приложенная сила i не очень велика и можно
пренебречь изменением толщины стержня, то
справедлив закон Гука:

где 6L — удлинение стержня, L_o — длина стержня
до деформации. Коэффициент Е,

характеризующий упругие свойства материала
стержня, называется модулем Юнга.

Применительно к пружине закон Гука
записывается в виде:

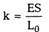
где

и х = 5L — абсолютное удлинение

пружины. Силами упругости являются и так
называемые силы натяжения нити Т и реакции
опоры N.

5. Закон сохранения импульса

Импульсом материальной точки называется
векторная величина, равная произведению ее
массы m на вектор скорости частицы v:

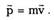
Из первого закона Ньютона следует, что
импульс свободной частицы не изменяется ни по
величине, ни по направлению, т.е. р = const. Если

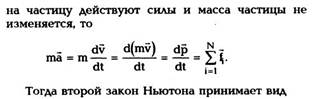
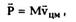
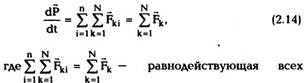
Переписав (2.11) в виде

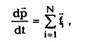
(2.8)

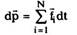
т.е. скорость изменения импульса частицы dp/dt
равна векторной сумме сил, действующих на нее.
Из (2.8) следует, что изменение импульса частицы
за время dt

систему взаимодействуют только между собой и
не взаимодействуют с телами, не входящими в
систему, то такая система называется замкнутой.
В противном случае система не является
замкнутой.

Импульсом системы Р называется векторная
сумма импульсов всех частиц, входящих в
систему:

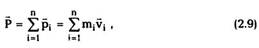
где т, — масса i-ой частицы и Vj - ее скорость в

выбранной ИСО. С течением времени импульсы
частиц изменяются, а сами частицы движутся по
каким-то своим траекториям Fj = Г|(1).

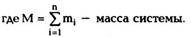
Центром масс (центром инерции) системы
частиц называется точка в пространстве, радиус-
вектор которой определяется из выражения:

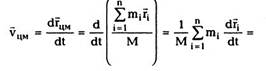
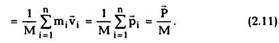
Найдем теперь скорость, с которой движется
центр масс системы. По определению вектора
скорости

внешних сил, действующих на систему.
Соотношение (2.14) называется вторым законом
Ньютона для системы материальных точек:

скорость изменения импульса системы равна
векторной сумме внешних сил, действующих на
систему.

Используя (2.12), уравнение (2.14) можно,
переписать в виде

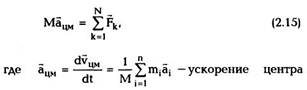
масс системы и а₄ - ускорение i-ой частицы. Из

(2.15) видно, что второй закон Ньютона для
системы частиц по форме совпадает со вторым
законом Ньютона для материальной точки, только
вместо массы частицы стоит масса системы,
вместо ускорения частицы — ускорение центра
масс, а в правой части — не все, а только
внешние по отношению к системе силы.
Уравнение (2.14) можно записать в виде

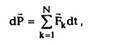
где dP — бесконечно малое изменение импульса
системы за время dt под действием импульсов

внешних сил F_kdt, то есть импульс системы могут
изменить только импульсы внешних сил.

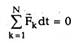
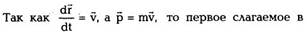
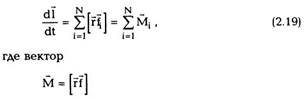
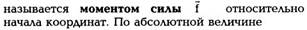
Если система замкнутая, то

и dP = 0, то есть импульс замкнутой системы:

Это утверждение носит название закона
сохранения импульса. Этот закон является одним
из фундаментальных законов природы и вытекает,
вообще говоря, из свойств нашего пространства, а
именно, из свойства однородности пространства:
физические процессы, протекающие в замкнутой
системе, не зависят от положения системы в
пространстве.

Из соотношения (2.15) следует, что центр масс
замкнутой системы движется равномерно и

6. Закон сохранения момента
импульса

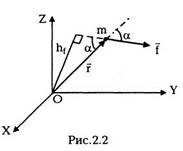
Помимо импульса р = mv, материальная точка
характеризуется еще одной динамической
переменной, которая называется моментом

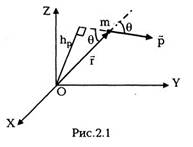
импульса. Моментом импульса частицы I
относительно начала координат называется
векторная величина

где квадратные скобки обозначают векторное
произведение. По модулю

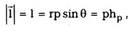
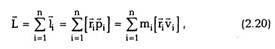
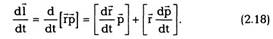
Из (2.21) видно, что для замкнутой системы

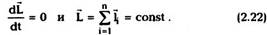
Это утверждение называется законом
сохранения момента импульса. Как и закон

сохранения импульса, этот закон вытекает из
свойства нашего пространства, которое
называется изотропностью пространства:
явления, протекающие в замкнутой системе, не
изменяются при повороте всей системы в
пространстве.

Дата добавления: 2013-12-12