Эквивалентность массы и энергии

Рассмотрим теперь неупрутое столкновение
двух частиц. Предположим, что две одинаковые
частицы массой m движутся в системе К
навстречу друг другу вдоль оси ОХ с одинаковыми
скоростями v. Тогда

После столкновения они слипаются, образуя
новую частицу. Так как до столкновения

новая частица после столкновения покоится

то есть масса новой частицы М превысила
исходную массу 2т на

В другой системе К', движущейся
относительно К со скоростью и:

Подставляя (9.13) в (9.17), получим

так как кинетическая энергия превратилась в
массу. Изменение массы AM, связанное с
превращением кинетической энергии в массу, в
повседневных процессах обычно очень мало и не
поддается измерениям.

имеющих

Так, при столкновении и слипании двух

шариков массой

добавочная

одинаковые по величине и противоположные по

направлению скорости

масса

С учетом (9.15), (9.16) имеем

Этот результат свидетельствует о том, что в
СТО, в отличие от ньютоновской механики,
энергия при неупругом столкновении сохраняется.

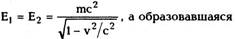
Поскольку

частица покоится, то есть Е₃ — ее энергия покоя,
мы вынуждены на основании (9.19) утверждать,
что масса образовавшейся частицы М>2т, так как
из (9.19) следует, что

Мы получили новый важный результат: в СТО,
в отличие от механики Ньютона, нет закона
сохранения массы системы частиц - она может
возрастать или уменьшаться, в зависимости от
того, какие превращения происходят с
кинетической энергией входящих в систему
частиц. В данном примере кинетическая энергия

после

исходных частиц

Эта величина значительно меньше ошибки, с
которой может быть измерена масса в 1г.

Совсем другая ситуация наблюдается в
процессах, происходящих внутри атомного ядра,
состоящего из элементарных частиц протонов и
нейтронов, массы которых хорошо известны:

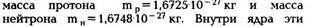
частицы удерживаются так называемыми
ядерными силами. Так, ядро тяжелого водорода
(дейтерия) состоит из одного протона и одного

Откуда взялась эта разница? Дело в том, что
для разделения ядра дейтерия на протон и
нейтрон необходимо затратить энергию, чтобы
преодолеть мощные ядерные силы,

удерживающие эти частицы в ядре. Эта энергия
называется энергией связи ядра. Для ядра
дейтерия экспериментально измеренная энергия
связи Е_св = 2,226 МэВ. Разделяя ядро дейтерия, мы
увеличиваем массу ядра на величину

столкновения обратилась в нуль, то есть
изменилась на

или, на основании (9.20),

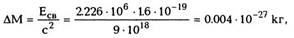
что совпадает с (9.22).

Взаимное превращение энергии и массы
играет фундаментальную роль в ядерных
реакциях деления и синтеза. Так, например,
важнейшим источником энергии Солнца и
большинства звезд является ядерное "сжигание"
протонов с образованием ядер гелия.

Лекция 10. ВВЕДЕНИЕ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКУЮ
ТЕОРИЮ

Количество вещества; абсолютная температура, макроскопические
параметры; основное уравнение кинетической теории идеального газа,
уравнение состояния идеального газа.

Число молекул в одном моле получается делением молярной массы (10.4) на массу одной молекулы (10.3)

Дата добавления: 2013-12-12