Метод простой итерации

Итерационные методы уточнения корней

Графическое отделение корней

Очевидно, что найти корень уравнения (1) означает найти абсциссу точки пересечения графика y = f (x) с прямой у = 0, т.е. осью абсцисс. При этом если построение y = f (x) затруднительно, то ее представляют в эквивалентном виде:

f ₁(x) = f ₂(x) (3)

с таким расчетом, чтобы графики y ₁ = f ₁(x) и y ₂ = f ₂(x) строились проще. Абсциссы их точек пересечения и будут корнями уравнения (1).

Рассмотрим в качестве примера уравнение x ³ – 3 x – 0,4 = 0. Согласно (3) запишем его как

x ³ = 3 x + 0,4. (4)

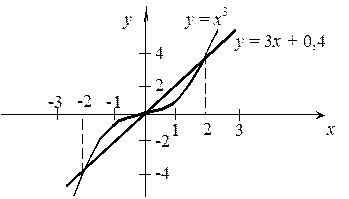
Из рисунка видно, что здесь три корня: с ₁ Î [ – 2, –1]; с ₂ Î [ – 1, 0]; с ₃ Î [1, 2].

При графическом отделении корней уравнения результат зависит от точности построения графиков.

Метод простой итерации применяется к решению уравнения (1), разрешенному относительно x:

x = j(x). (5)

Переход от записи (1) к эквивалентной записи (5) можно сделать многими способами.

Метод состоит в построении последовательности (2) в виде:

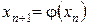, n = 0,1,2,….

Если j(x_n) – непрерывная функция, а x_n – сходящаяся последовательность, то искомое значение x * =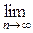 x_n и будет решением (5), а, следовательно, и (1).

Например, получим (5) из (1) следующим образом: умножим (1) на подобранную специальным образом функцию y(x) ¹ 0 (в частности можно взять y(x) = const) и сложим с тождеством x = x, тогда (5) будет иметь вид, эквивалентный виду (3):

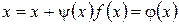. (6)

Подбирая y(x) добиваются сходимости решения (6). Она может быть монотонной (если j ' (x) > 0), или колеблющейся (если j ' (x) < 0).

Метод, очевидно, является одношаговым (m =1) и для начала вычислений нужно знать одно начальное приближение x ₀ = a, или x ₀ = b, или x ₀ = (a+b)/2.

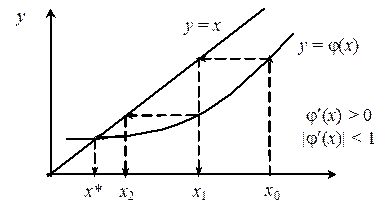
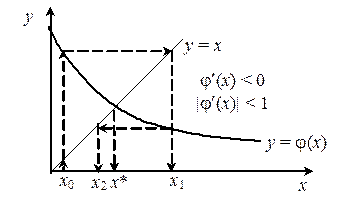
В методе простой итерации сходимость гарантированна не всегда, например, если j(x) имеет такой характер:

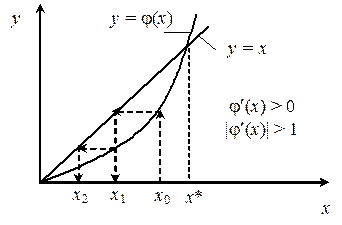
Такая ситуация может быть устранена подбором y(x) в (6).

Что касается выбора y(x), то можно взять, например, y(x) = Const = 1/ k. В этом случае необходимо, чтобы | k | > max| f ¢(x)| / 2. При этом знак k должен совпадать со знаком f ¢(x).

Доказано, что в общем случае расходимость (несходимость) исключается, если подбирается соотношение

| j'(x) | £ q < 1. (7)

При этом скорость сходимости увеличивается при уменьшении величины q.

Максимальный интервал (a, b) при выполнении условия (7) называется областью сходимости. Для данной оценки (7) берется любое x Î (a,b); x* Î(a,b).

Итерационный процесс уточнения корня заканчивается, когда {| x_n – x_{n –1}| или | f (x_n) – f (x_{n –1})|} < e.

Дата добавления: 2013-12-11