Метод секущих

Метод Ньютона (касательных)

Данный метод является модификацией метода простой итерации. Если функция f (x) непрерывна и дифференцируема, то выбрав в (6) 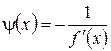получим эквивалентное уравнение в виде x = x – f (x)/ f '(x) = j(x), f '(x) ¹ 0.

Подбором y(x) добиваются, чтобы в (7) q = j'(x^*) º 0, что обеспечивает большую скорость сходимости в рекуррентном соотношении метода в близи искомого корня

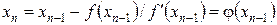, n = 1,2,… (8)

Это также одношаговый метод.

Геометрическая интерпретация метода представлена на рисунке.

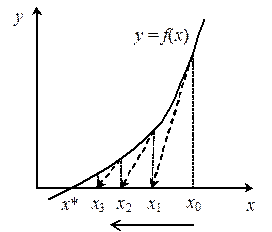
Проблематичным является выбор x ₀ в виду узости области сходимости вычисления производной. Часто при неудачном выборе x ₀ нет монотонного убывания последовательности | f (x_n)|, поэтому рекомендуется вычисления проверить по модифицированной схеме

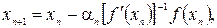n = 0,1,2,…

Здесь сомножители a _n Î [0,1] выбирают так, чтобы выполнялось неравенство

| f (x_{n +1})| < | f (x_n)|.

При выборе начального приближения х ₀ предпочтительней использовать заведомо сходящийся метод, например, метод деления отрезка пополам.

Этот метод является модификацией метода Ньютона в плане его реализации, т.е. задача поиска корня связана лишь с вычислением значения функции f (x). Заменив производную f ' (x_n) в методе Ньютона так называемой разделенной разностью по двум точкам x_n и x_n + h_n, где h_n – некоторый малый параметр, получим итерационную формулу

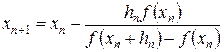, n = 0,1,2,…, (9)

которая называется методом секущих.

Приближение x_{n +1} является абсциссой точки пересечения секущей прямой, проведенной через точки (x_n, f (x_n)) и (x_n + h_n, f (x_n + h_n)) с осью х.

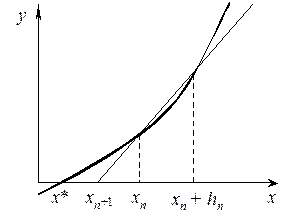
Метод также одношаговый и при удачном подборе параметра h его сходимость, как и у метода Ньютона при упрощении его реализации.

Имеются другие интерпретации формулы (9). В частности, метод Вегстейна,в котором для выбора параметра h используют предыдущую расчетную точку, т.е. берут h_n = x_{n –1} – x_n, тогда (9) имеет вид:

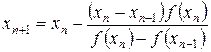, n = 0,1,2,… (10)

Метод Вегстейна, очевидно, двухшаговый (m = 2), т.е. для вычисления требуется задать 2 начальные точки приближения, лучше всего x ₀ = а; x ₁ = b. Он медленнее метода секущих, однако, требует в 2 раза меньше вычислений f (x) и поэтому оказывается более эффективным.

Целесообразным является использовать подходы к уточнению корня не выпускающие корень из выделенной «вилки», (отрезка [ a, b ]).

Так, если f (b)× f "(x) > 0 для x Î [ a, b ], берут в качестве x ₀ = a и уточнение ко­рня производится по формуле

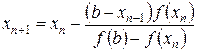, n =0,1,2,…, (11)

а если f (a)× f "(x) > 0 для x Î [ a, b ], берут в качестве x ₀ = b и уточнение корня производится по формуле

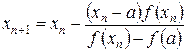, n =0,1,2,… (12)

Дата добавления: 2013-12-11