Метод хорд

Метод деления отрезка пополам

Все вышеизложенные методы могут работать, если функция f (x) из (1) является непрерывной и дифференцируемой вблизи искомого корня, в противном случае решение не гарантируется. Данный метод может быть использован даже для разрывных функций.

Его алгоритм реализовывается согласно следующей рекуррентной последовательности: для x ^*Î [a,b]; x ₀ = a; x ₁ = b, находится x ₂ = (a+b)/2.

Очередная точка x ₃ выбирается как середина того из смежных с x ₂ интервалов [ x ₀, x ₂] или [ x ₂, x ₁], на котором находится корень. В результате получается следующий алгоритм метода деления отрезка пополам:

1) вычисляем y ₀ = f (x ₀);

2) вычисляем ;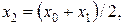

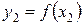3) если 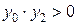, тогда x ₀ = x ₂, иначе x ₁ = x ₂; (13)

4) если 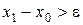, тогда повторять с п. 1;

5) вычисляем .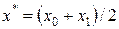

За одно вычисление функции погрешность уменьшается вдвое, т.е. скорость сходимости невелика, однако метод устойчив к ошибкам округления и всегда сходится.

Немного подкорректировав алгоритм (13), его более наглядно можно представить в виде блок-схемы:

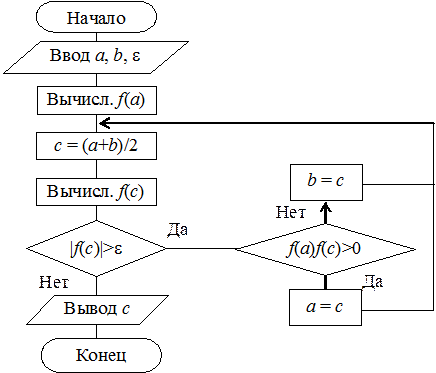
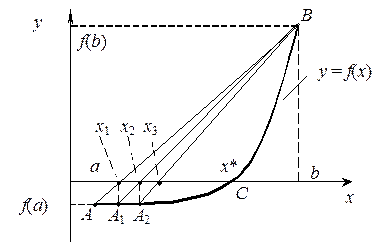
Пусть корень С уравнения f (x)=0 отделен на [ a, b ]. Функция f (x) непрерывна на отрезке и на его концах имеет разные знаки. Точки А и В имеют координаты соответственно (a, f (a)) и (b, f (b))

Искомым корнем С будет пресечение f (x) с осью ОХ. В начале итераций вместо С ищется приближение x ₁, как результат пересечения ОХ с хордой АВ.

Уравнение прямой АВ запишем в виде .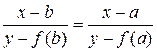

Полагая у = 0, находим 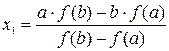. Это можно записать в виде:

или 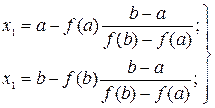(14)

Если x ₁ оказывается недостаточно точным, находят второе приближение:

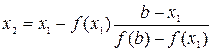. (15)

На основании (14) и (15) можно записать рекуррентную последовательность:

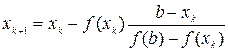, (16)

если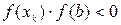, и

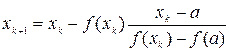(17)

если.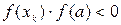

Заметим, что на выделенном интервале [ a, b ] имеют место четыре типа расположения кривой f (x).

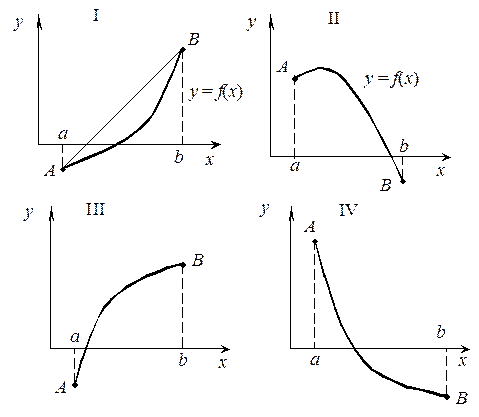
Для I-го f ' (x) > 0, f " (x) > 0, для II-го f ' (x) < 0, f " (x) < 0, для III-го f ' (x) > 0, f " (x) < 0; для IV-го f ' (x) < 0, f " (x) > 0.

Тогда для I-го и для II-го используется (16), т.е. х ₀ = а. Для III-го и IV-го используется (17), т.е. х ₀ = b.

В заключение заметим, что во всех методах для определения функции f (x) и ее производных целесообразно использовать схему Горнера.

Дата добавления: 2013-12-11