Метод простой итерации

Постановка задачи

Раздел 4. Решение систем нелинейных уравнений

Общий алгоритм численных методов решения нелинейных уравнений

Рассмотрим реализацию двух этапов их решения.

1. Программа должна сначала выдать таблицу значений y = f (x) (отделений корней).

2. Далее делается запрос на ввод начального приближения (это a, b или (a+b)/2) и точности решения e.

Расчет функции и вычислительный алгоритм обычно выполняются в виде отдельных подпрограмм.

Примерный алгоритм данных процедур может иметь следующий вид:

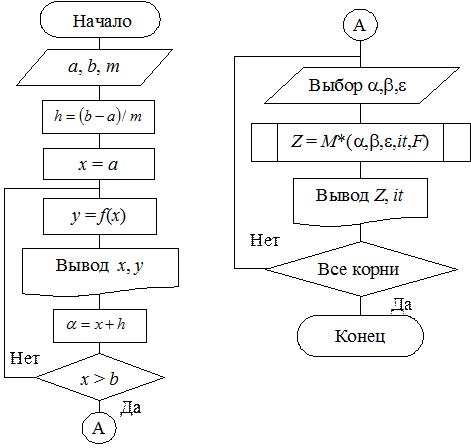
Значение m выбираем по усмотрению, но с соблюдением принципа «половинного деления», рассмотренного выше.

Многие практические задачи сводятся к решению систем нелинейных уравнений с n неизвестными:

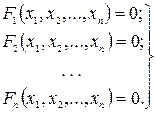(1)

В отличие от линейных систем прямых методов их решения нет за исключением систем второго порядка, когда одно неизвестное может быть выражено через другое.

Наиболее распространены два метода: метод простой итерации и метод Ньютона.

Система (1) должна быть представлена в следующем виде:

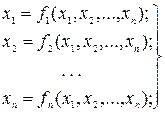(2)

где 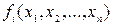называются итерирующими функциями.

Алгоритм решения аналогичен алгоритму Зейделя или простой итерации для решения систем линейных уравнений.

Пусть известен начальный вектор решения: x_i = a_i, i = 1,2,…, n, тогда

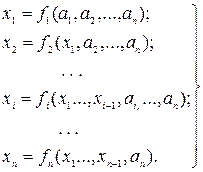
Итерационный процесс продолжается до тех пор, пока изменение всех неизвестных в двух последовательных итерациях не станет меньше заданного значения e.

Начальные значения должны быть близкими к истинным значениям, иначе итерационный процесс может не сойтись. Стоит проблема их отыскания (т.е. условий сходимости). В случае расходимости (несходимости) в блок-схеме алгоритма срабатывает механизм ограничения числа итераций.

Дата добавления: 2013-12-11