Вблизи абсолютного нуля все процессы протекают без изменения энтропии!

Вблизи абсолютного нуля энтропия абсолютно правильного бездефектного кристалла равна нулю!

III Закон Термодинамики

Данный закон состоит из двух постулатов:

1. Постулат Планка:

2. Тепловая теория Нернста:

Математическую формулировку данного закона можно представить в виде формулы:

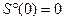
III Закон Термодинамики показывает условие, при котором энтропия равна нулю, то есть дает начало отчета энтропии и позволяет рассчитать её абсолютное значение.

Очевидно, что абсолютный «нуль» температур невозможен, однако постулатом Планка можно пользоваться без особых ограничений, так как он лишь фиксирует начало отчета!

Расчет абсолютных значений энтропии

В общем случае расчет сводится к суммированию изменений энтропии на определенных участках, которые проходит система для достижения определенной температуры.

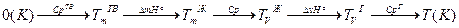
нагрев. плавл. нагрев. испарен. нагрев.

температура температура

плавления кипения

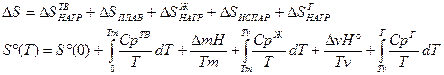
Данная формула позволяет рассчитать абсолютные значения энтропии 1 моль вещества, находящегося при температуре Т в газообразном состоянии.

Для многих веществ посчитаны энтропии при стандартных условиях, поэтому

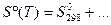
При расчете абсолютных энтропий твердых тел вблизи абсолютного нуля используется температурный ряд теплоемкостей в виде кубического полинома (многочлена)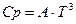

Данная зависимость хорошо работает до температуры T=80K, поэтому второе слагаемое чаще всего разбивают на два: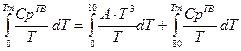

Применение III Закона Термодинамики к химическим реакциям

Так как для большого количества веществ абсолютные энтропии табулированы, то с помощью III Закона Термодинамики можно рассчитать изменение энтропии в результате химической реакции по абсолютным значениям энтропии:

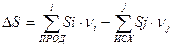
Если реакция протекает при температуре, отличной от стандартной, то изменение энтропии будет находиться, как

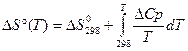
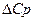может быть заменено изменением средней теплоемкости. В этом случае после подстановки средней теплоемкости и интегрировании получаем:

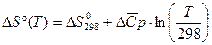
Так же 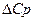может быть заменено температурным рядом. Тогда:

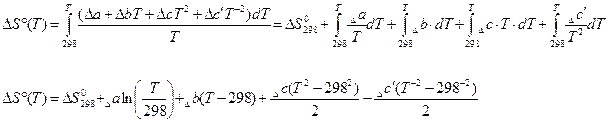
Термодинамическое описание закрытых систем с постоянным составом.

термодинамические потенциалы

Термодинамический потенциал – термодинамическая функция, показывающая направление процесса, то есть возможность самопроизвольного протекания химических реакций в выбранном направлении.

Первым термодинамическим потенциалом служила энтропия. К сожалению, этот критерий направленности работает только в изолированных системах и не применим к реальным системам.

Теплота, выделяющаяся или поглощающаяся в ходе химической реакции так же не может служить критерием направленности, поэтому основным критерием направленности процесса была принята работа.

а) Если работа совершается системой, W>0(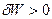), процесс считается самопроизвольным.

б) Если работа совершается над системой, процесс считается не самопроизвольным W<0, (),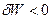

Однако, использовать работу в качестве критерия направленности не очень удобно, так как она является функцией процесса и будет зависеть от пути процесса.

Таким образом, термодинамический потенциал – функция, связанная с работой и являющаяся критерием направленности процесса, то есть функцией состояния!

Очевидными, критерием направленности является изменение внутренней энергии и энтальпии. Однако, данные критерии будут реализовываться только в специфических условиях.

Запишем объединенное уравнение I и II Закона Термодинамики

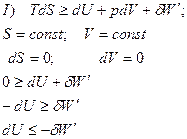
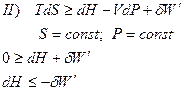
Вывод: Для того, чтобы изменение энтальпии или внутренней энергии служили критериями направленности процесса, необходимо постоянство энтропии, чего в реальных условиях добиться невозможно!

Для реальных процессов были выбраны другие критерии направленности.

I) Изохорно-изотермический процесс:

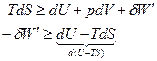
U-TS=A(F) – Свободная энергия Гельмгольца

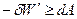
Таким образом, свободная энергия Гельмгольца является критерием направленности процесса в изохорно-изотермических условиях. Поэтому её называют ' Изохорно-изотермическим потенциалом '.

Таким образом, самопроизвольный процесс в изохорно-изотермических условиях будет считаться процесс с уменьшением энергии Гельмгольца.

Если над системой совершается насилие (работа), то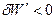

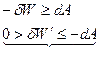
То процесс считается не самопроизвольным!

II) Изобарно-изотермический процесс:

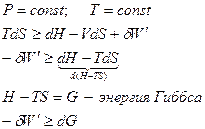
Самопроизвольным считается процесс в изобарно-изотермических условиях, идущий с уменьшением энергии Гиббса.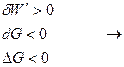

Для не самопроизвольного процесса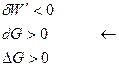

Для состояния равновесия

Вывод: Таким образом, исходя из объединенного уравнения I и II Закона Термодинамики, можно сделать вывод, что в изохорно-изотермических условиях в качестве критерия самопроизвольности процесса выступает энергия Гельмгольца; в изобарно-изотермических условиях – энергия Гиббса.

Если изменение Энергии Гиббса в изобарно-изотермических условиях или энергии Гельмгольца в изохорно-изотермических условиях меньше нуля, процесс считается самопроизвольным.

Если изменение этих же самых величин больше нуля, это свидетельствует о невозможности самопроизвольности данного процесса.

Если изменение этих же самых величин равны нулю, это свидетельствует о нахождении системы в состоянии равновесия.

Введенные величины, G и A связаны с понятием энтропии, поэтому говорят, сто энтропия выражает основное свойство природы – односторонность протекания процессов!

Свойства термодинамических потенциалов

Все свойства термодинамических потенциалов основаны на свойствах полного дифференциала и первой производной. Дифференцирование любого термодинамического потенциала проводится по естественным переменным, то есть тем величинам, которые должны сохраняться постоянными для придания работе свойств функции состояния.

Дата добавления: 2013-12-12