Тема № 2. Сложные проценты

В средне и долгосрочных финансово-кредитных операциях применяют сложные проценты. База для начисления сложных процентов (в отличие от простых) не остается постоянной - она увеличивается с каждым шагом во времени, абсолютная сумма начисляемых процентов возрастает, и процесс увеличения суммы долга происходит с ускорением. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называют капитализацией процентов.

Наращенная сумма по сложным процентам вычисляется по уравнению:

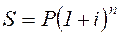, (2.1)

где

S - наращенная сумма;

P - первоначальный размер долга (ссуда, кредит и т.д.);

i - процентная ставка;

n - число лет наращения.

Пример: Какой величины достигнет долг, равный 1 млн. руб. через пять лет при росте по сложной ставке 15,5% годовых?

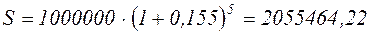руб.

Формула (2.1) предполагает постоянную ставку на протяжении всего

срока начисления процентов. Неустойчивость кредитно-денежного рынка заставляет модернизировать <классическую> схему, с помощью применения плавающих ставок. В этом случае общий множитель наращения определяется как произведение частных множителей:

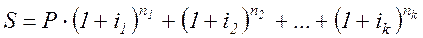
где

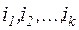- последовательные во времени значения ставок;

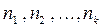- периоды, в течении которых <работают> соответствующие ставки.

Пример: Срок ссуды - 5 лет, договорная процентная ставка 12% годовых плюс моржа 0,5% в первые два года и 0,75% в оставшиеся.

.

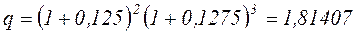Часто срок для начисления процентов не является целым числом. В

правилах ряда коммерческих банков для некоторых операций в этих случаях, проценты начисляются только за целое число лет. В большинстве же случаев учитывается полный срок. При этом применяются два метода. Согласно первому (общему), расчет ведется непосредственно по формуле (2.1). Второй, смешанный метод предполагает начисление процентов за целое число лет по формуле сложных процентов и по формуле простых процентов за дробную часть периода:

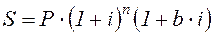(2.2)

где a + b = n

a - целое число периодов

b - дробная часть периода.

Для сопоставления результатов наращения по разным процентным ставкам достаточно сравнить соответствующие множители наращения. Нетрудно убедиться в том, что при одинаковых уровнях % ставок соотношения этих множителей существенно зависит от срока. Для срока меньше года:

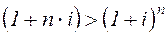, (2.3)

для срока больше года:

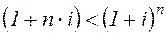, (2.4)

Различия в последствиях применения простых и сложных процентов

наиболее наглядно проявляется при определении времени, необходимого для увеличения первоначальной суммы в N раз.

Для простых процентов:

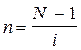, (2.5)

Для сложных процентов:

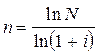, (2.6)

Номинальная ставка

В современных условиях проценты капитализируются не один, а несколько раз в году - по полугодиям, кварталам и т.д. Некоторые зарубежные коммерческие банки практикуют даже ежедневные начисления процентов. При начислении % несколько раз в году можно воспользоваться формулой (2.1), параметр n в этих условиях будет означать число периодов начисления, а под ставкой i следует понимать ставку за соответствующий период. В контрактах фиксируется не ставка за период, а годовая ставка в % и указывается период начисления %.

Пусть годовая ставка равна j, а число периодов начисления в году равно m. Проценты начисляют по ставке j/m. Ставку j называют номинальной.

Формулу наращения можно представить следующим образом:

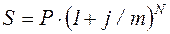, (2.7)

Пример: Какова сумма долга через 25 месяцев, если первоначальная

величина 500 тыс. руб., проценты сложные, ставка 20 % годовых, начисляются поквартальные.

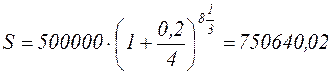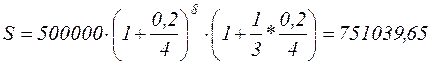руб.

руб.

Эффективная ставка.

Эффективная ставка – это годовая ставка сложных процентов, которая дает тот же результат, что и m-раззовое начисление процентов по ставке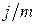

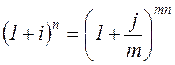
откуда

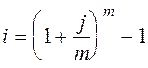, (2.8)

При m>1, эффективная ставка (i) больше номинальной (j) при m=1; i=j.

Замена в договоре номинальной ставки j при m-разовом начислении процентов на эффективную ставку i не изменяет финансовых обязательств участвующих сторон т.е. обе ставки эквивалентны в финансовом отношении.

Дисконтирование по сложной ставке процентов.

Применим математическое дисконтирование по сложной ставке процента. На основе (2.1) получим:

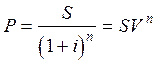, (2.10)

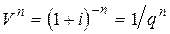, (2.11)

Величину 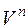называют дисконтным множителем. Для случаев, когда проценты начисляются m раз в году, получим:

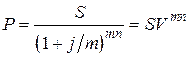, (2.12)

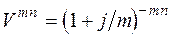, (2.13)

Величину Р, полученную дисконтированием S, называют современной стоимостью S. Разность S-P, в случае когда Р определено дисконтированием, называют дисконтом (D). ;

.

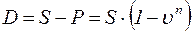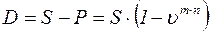Операции со сложной учетной ставкой.

В практике учетных операций иногда применяют сложную учетную ставку. Дисконтирование по сложной учетной ставке осуществляется по формуле:

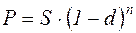, (2.14)

где d- сложная учетная ставка.

Дисконтирование по сложной учетной ставке выгоднее для должника, чем дисконтирование по простой учетной ставке. сказанное становится понятным при сравнении формул для дисконтных множителей:

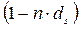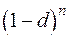и , где 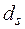- простая, d - сложная учетная ставка. Согласно первой формуле значение дисконтного множителя равномерно уменьшается по мере роста n и достигает нуля при 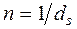, согласно второй множитель экспоненциально уменьшается и достигает нуля лишь в пределе, при .

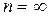Номинальная и эффективная учетная ставка.

По аналогии с номинальной и эффективной ставкой процентов вводится понятие номинальной и эффективной учетной ставки:

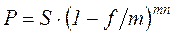, (2.15)

f - номинальная годовая учетная ставка.

Эффективная учетная ставка характеризует результат дисконтирования за год. Она находится из равенства

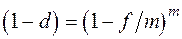
откуда .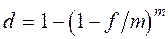

Для одних и тех же условий операций эффективная учетная ставка меньше номинальной.

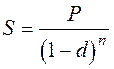, (2.16) или 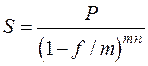, (2.17)

Непрерывные наращение и дисконтирование - непрерывные проценты.

В практических финансово-кредитных операциях непрерывное наращение, т.е. наращение за бесконечно малые отрезки времени, применяется крайне редко.

Существенно большее значение непрерывное наращение имеет в анализе сложных финансовых проблем, например, при обосновании и выборе инвестиционных решений, в финансовом проектировании.

При непрерывном наращении процентов применяют особый вид процентной ставки - силу роста. Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени.

При дискретном начислении процентов m раз в году по номинальной ставке j наращенная сумма определяется по уравнению:

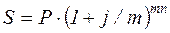
При 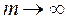именем:

,

,

.

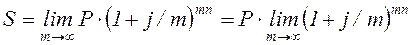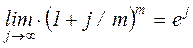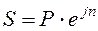Для того, чтобы отличить непрерывную ставку от дискретной, силу роста обозначают, как 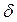, тогда:

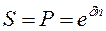, (2.18)

Дискретные и непрерывные ставки наращения находятся в функциональной зависимости между собой. Из равенства множителей наращения 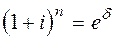следует:

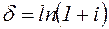, (2.19)

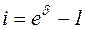, (2.20)

Пример. Сумма, на которую начисляются проценты, равна 2 млн. руб., сила роста - 10 %, срок - пять лет, наращенная сумма составит:

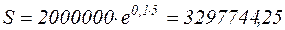руб.

Непрерывное наращение по ставке 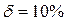равнозначна наращению за тот же срок сложных годовых % по ставке

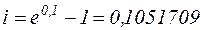или 10,517090 %.

Дисконтный множитель на основе силы роста находится из уравнения (2.18)

.

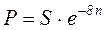Дисконтный множитель = .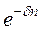

Переменная сила роста.

Пусть сила роста изменяется во времени, следуя определенному закону - непрерывной функции времени: 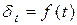, тогда наращенная сумма и сохраненная стоимость определяются по уравнениям:

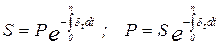
Рассмотрим варианты определения множителя наращения для случаев, когда величина 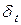представляет собой линейную и экспоненциальную функцию. Если это линейная функция 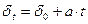, где 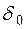- начальное значение силы роста, а - ее прирост, то

.

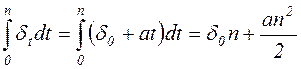Множитель приращения определяется по уравнению

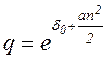, (2.21)

Рассмотрим ситуацию, когда сила роста изменяется по геометрической прогрессии: 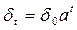, 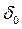- начальное значение силы роста, а - постоянный темп роста.

В этом случае:

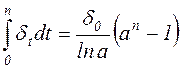
Сам множитель определяется по уравнению:

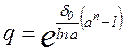, (2.22).

Определение срока платежа и процентных ставок.

При разработке условий финансовых операций часто бывает необходимо решить обратную задачу - определить продолжительность ссуды или определить уровень процентной ставки.

Срок платежа. Приведем формулы расчета n для различных условий наращения процентов и дисконтирования. При наращении по смежной годовой ставке i по номинальной ставке j, соответственно получим:

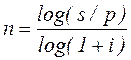, (2.23)

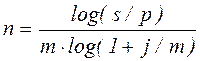, (2.24)

При дисконтировании по сложной годовой учтенной ставке d и по номинальной учтенной ставке f:

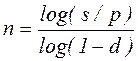, (2.25)

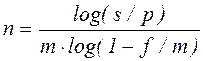, (2.26)

При наращении по постоянной силе роста 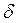и по изменяющейся с постоянным темпом силе роста:

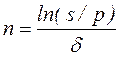, (2.27)

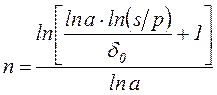, (2.28)

Величина процентной ставки.

Приведем формулы для расчета ставок i, j, f, 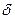для различных условий наращения процентов и дисконтирования.

При наращении по сложной годовой ставке процентов и по номинальной ставке m раз в году находим:

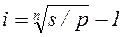
, (2.29) 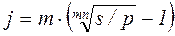, (2.30)

При дисконтировании по сложной учетной ставке и по номинальной учетной ставке,

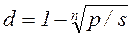, (2.31)

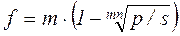, (2.32)

При наращении по постоянной силе роста

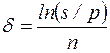, (2.33)

При наращении по изменяющейся с постоянным шагом силе роста

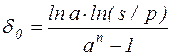, (2.34)

Кривые доходности.

Любая кредитная операция предполагает использование некоторого значения процентной ставки, с которой согласились обе стороны, участвующие в операции. Для практика важно представить себе зависимость изменения размера ставок в зависимости от различных факторов.

Наиболее важным фактором является срок операции. При всех прочих равных условиях ссуда на пять лет более рискованна, чем на два года и менее. Компенсировать риск владельцу денег может повышение доходности.

Существуют две конкурирующие теории объясняющие ²поведение² доходности - теория ликвидности и теория ожиданий. Первая изменение доходности связывает с увеличением риска ликвидности по мере увеличения срока. Согласно второй теории утверждается, что форма кривой может рассматриваться как обобщенная характеристика ожиданий инвесторов.

Конверсия валюты и наращение сложных %.

Рассмотрим схему:

СКВ ® Руб ® Руб ® СКВ

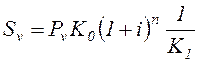, (2,35)

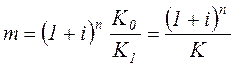; K - темп роста валюты.

Определим доходность операции в целом из уравнения (2,29)

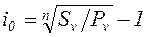, (2,36)

Подставив в эту формулу 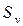получим:

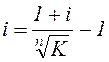, (2.37)

Максимально допустимое значение К при котором доходность операции будет равна доходности при прямом инвестировании валютных средств по ставке j определяется по уравнению:

.

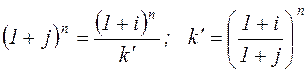Наращение процентов, налоги и инфляция.

Налоги на полученные проценты.

При начислении простых процентов

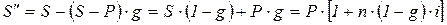
где 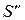- реально наращенная сумма,

g - ставка налога на %.

В долгосрочных операциях при начислении налога на сложные % возможны следующие варианты: налог начисляется на весь срок сразу или последовательно в конце каждого года. В первом случае:

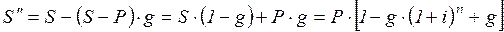, (2.38)

Во втором случае налог определяется за каждый истекший год. Сумма налогов за весь срок не зависит от метода начисления.

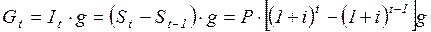, (2.39)

Инфляция.

Изменение покупательской способности денег за некоторый период измеряется с помощью индекса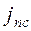

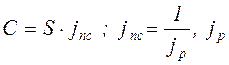- индекс цен.

Под темпом инфляции понимается относительный прирост цен за период (H), измеряется в %.

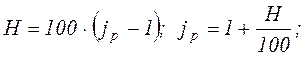
Например, если темп инфляции равен 130 %, то цены за этот период выросли в 2,3 раза.

Среднегодовые темп роста цен 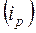и темп инфляции (h) находятся на основе величины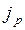

.

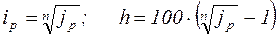Поскольку инфляция является цепным процессом (цены в текущем периоде, повышаются на 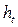% относительно уровня, сложившегося в предыдущий период), то индекс цен за несколько таких периодов равен произведению цепных индексов цен:

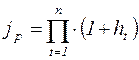; (2.40)

Если h - постоянный ожидаемый (или прогнозируемый) темп инфляции за период, то за n таких периодов получим:

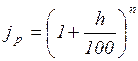, (2.41)

Рассмотрим проблему обесценивания денег при их наращении. В общем случае:

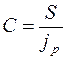, (2.42)

При наращении по простой ставке, имеем:

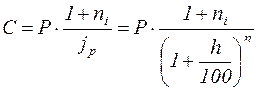, (2.43)

Увеличение наращенной суммы с учетом сохранения покупательной способности денег имеет место тогда, когда .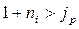

При наращении по сложным процентам

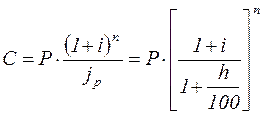, (2.44)

Если h/100 < i происходит малый рост. Ставка по простым процентам, которая только компенсирует инфляцию определяется по уравнению:

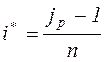
Для сложных процентов .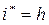

Ставку, превышающую 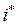, называют положительной ставкой процента.

Дата добавления: 2013-12-12