Тема № 4. Потоки платежей

Постоянные финансовые ренты.

Погашение за должности в рассрочку, периодическое поступление доходов от инвестиций, выплата пенсий и т.д. - называют потоки платежей.

Потоки платежей могут быть регулярными и нерегулярными. В нерегулярном потоке платежей членами являются как положительные (поступления), так и отрицательные величины (выплаты), а соответствующие платежи могут производится через разные интервалы времени.

Поток платежей, все члены которого положительные величины, а временные интервалы между платежами одинаковы, называют финансовой рентой или просто рентой.

Рента характеризуется следующими параметрами: член ренты - размер отдельного платежа, период ренты - временной интервал между двумя последовательными платежами, срок ренты - время от начала первого периода ренты до конца последнего периода, процентная ставка.

По количеству выплат членов ренты на протяжении года, ренты делятся на годовые, P - срочные (P - количество выплат в году), непрерывные (много раз в году).

Обобщенные параметры потоков платежей.

Анализ потока платежей предполагает расчет одной из двух обобщающих характеристик: наращенной суммы или современной стоимости.

Наращенная сумма - сумма всех членов потока платежей с начисленными на них к концу срока процентами.

Современная стоимость потока платежей - сумма всех его членов, дисконтированных на начало срока ренты или некоторый упреждающий момент времени.

Допустим, имеется ряд платежей , выплачиваемых спустя время после некоторого начального момента времени, общий срок

выплат n лет. Необходимо определить наращенную на конец срока сумму потока платежей, если проценты начисляются раз в году по сложной ставке i, то:

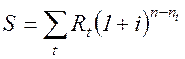, (4.1)

Как видим, наращенную сумму в заданных условиях получают методом прямого счета. Современную стоимость такого потока найдем прямым счетом - как сумму дисконтированных платежей. Обозначив эту величину, как A, получим:

, (4.2)

где 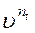- дисконтный множитель по ставке i.

Между величинами A и S существует функциональная зависимость:

, (4.3)

Наращенная сумма постоянной ренты постнумерандо.

Очень важным является различие рент по моменту выплат плате-

жей в пределах периода. Если платежи осуществляются в конце периодов, то такие ренты называют обыкновенными или постнумерандо, если же платежи производятся в начале периодов, то их называют пренумерандо.

Годовая рента.

В течении n лет в банк в конце каждого года вносится по R руб

На взносы начисляются сложные проценты по ставке % годовых. Все члены ренты, кроме последнего, приносят проценты - на первый член ренты начисляются (n-1) год, на второй (n-2) и т.д.

.

Если переписать этот ряд в обратном порядке, то получим геометрическую прогрессию со знаменателем (1+ i) и первым членом R.

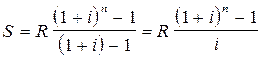, (4.4)

Обозначим ;

, (4.5)

При начислении процентов m раз в году:

, (4.6)

Пусть рента выплачивается Р раз в году равными суммами, про-

центы начисляются один раз в конце года тогда:

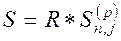, (4.7)

При p=m

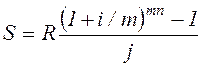, (4.8)

Современная стоимость постоянной ренты постнумерандо.

Рассмотрим годовую ренту постнумерандо, член которой равен R, срок ренты n, ежегодное дисконтирование. В этих условиях дисконтированная величина первого платежа равна , второго - ,

... последнего -

, (4.9)

Множитель на который умножается R называется коэффициентом приведения ренты и обозначается

При , (4.10)

Пример. Рента постнумерандо характеризуется следующими пара

метрами: R = 4 млн. руб., n = 5.

При дисконировании по сложной ставке процента, равной 18,5%

годовых получим:

млн. руб., т.е. 12,368 млн.руб. размещенных под 18,5% годовых, обеспечивают ежегодную выплату по 4 млн. рублей в течении 5 лет.

Годовая рента, начисление процентов m раз в году:

, (4.11)

Рента p-срочная (m=1).

, (4,12)

Рента р - срочная (р=m)

, (4.13)

Сравнение современных постоянных стоимостей рент

постнумерандо с разными условиями.

Величина современной стоимости заметно зависит от условий наращения процентов (точнее дисконирования) и частоты выплат в течении года.

Если обозначить современные стоимости:

А (p;m), причем (1;1) - годовая рента с ежегодным начислением процентов, (p; ¥) - p-срочная рента с непрерывным начислением процентов.

Для одних и тех же годовых сумм выплат и процентных ставок

(i =j =d) получим:

A(1; ¥) < A(1;m) < A(1;1) < A(p; ¥) <

<A(p;m) < A(p;m) < A(p;m) < A (p;1).

m>p>1 p=m>1 p>m>1.

Зависимость между наращенной и современной стоимостьюпостоянной ренты.

Для годовых и p-срочных постоянных рент постнумерандо с ежегодным начислением %

, (4.14)

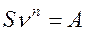, (4.15)

Для рент с начислением процентов m раз в году:

, (4.16)

, (4.17)

Определение параметров постоянных рент постнумерандо.

Определение члена ренты.

Исходные условия: задается S или A и набор параметров, кроме R

Из формулы (4.5).

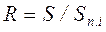, (4.18)

И формулы (4.9.)

, (4.19)

Расчет срока ренты.

Кол-во Кол-во S A

платежей начислений

в году в году

m=1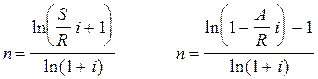

p=1

m>1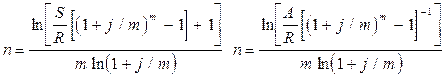

------------------------------------------------------------------------------

m=1

P>1

m=p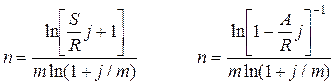

m¹p

При расчете срока ренты необходимо принять во внимание следующие моменты:

1. Расчетные значения срока будут дробные. Для годовой ренты в качестве n удобнее принять меньшее ближайшее число. У p-срочной ренты результат округляется до ближайшего целого числа периодов - np. Например, для квартальной ренты получено n = 6,28 года, откуда np = 25,12 квар. Округляем до 25, в этом случае n = 6,25 года.

2. Если округление производится до меньшего целого числа, то наращенная сумма или современная стоимость ренты оказывается меньше заданной. Возникает необходимость в соответствующей компенсации. Например, если речь идет о погашении за должности путем выплаты постоянной ренты, то компенсация может быть осуществлена соответствующими платежом в начале или конце срока или с повышением суммы члена ренты.

Определение размера % ставки.

Расчет процентной ставки по остальным параметрам ренты не так прост, приходится применять итерационные методы (например, Ньютона - Рафаона).

С помощью этого метода последовательным приближением решает-

ся нелинейное уравнение f(x)=0. Общий вид рекурентного соотношения

, (4.20)

где k - номер итерации.

Приняв в уравнении (4.4) q=1+i, получим

;

или ;

;

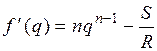, (4.21)

Начальное значение q выбирают так, чтобы было близко к

заданной величине отношения .

Аналогичным путем определяют функцию и ее производную, когда заданной является современная стоимость ренты:

,

.

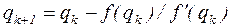Наращенные суммы и современные стоимости других видов

постоянных рент.

Различие между рентами постнумерандо и пренумерандо заключается в числе периодов начисления процентов. Легко понять что каждый член последней из указанных рент "работает" на один период больше, чем в ренте постнумерандо.

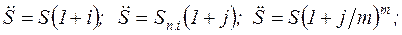
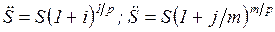и т.д.

Важным частным случаем является рента с платежами в середине периода. В этом случае умножение производится на .

Отложенные ренты.

Современная стоимость отложенной ренты равна дисконтированной величине современной стоимости немедленной ренты:

, (4.22)

Пусть годовая рента постнумерандо делится между двумя участниками (наследниками). Рента имеет параметры: Условия деления: а) каждый участник получает 50 % капитализированной стоимости ренты;

б) рента выплачивается последовательно с начало первому, затем второму участнику. Определить срок получения ренты первым участником.

;

;

;

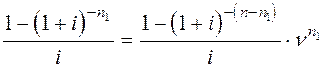, (4.23)

Постоянные непрерывные ренты.

Предложение о непрерывности ренты увеличивает возможности количественного анализа производственных долгосрочных инвестиций. Приведем уравнения для вычислений коэффициента приведения и коэффициента наращения, без вывода:

, (4.25)

, (4.26)

Очевидно, переход от дискретных взносов постнумерандо к непрерывным увеличивает соответствующие коэффициенты в i / ln(1+i) раз.

.

Пример. Ожидается, что доходы от эксплуатации месторождения полезных ископаемых составит 1 млрд. руб. в год, продолжительность разработки - 10 лет, отгрузка и реализация продукции непрерывная и равномерная. Капитализированная стоимость дохода при дисконтировании по ставке 10 % составит:

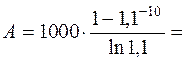6446,91 млн. руб.

Формулы (4.25) и (4.26) предполагают непрерывное поступление платежей и дискретное начисление процентов. Для получения формул для непрерывных процентов, вспомним, что

сила роста:

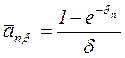, (4.27)

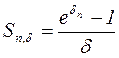, (4.28)

Определение срока и размера ставки для постоянных

и непрерывных рент.

Определим n (срок) из (4.27) и (4.28)

, (4.29)

, (4.30)

Сила роста определяется по методу Ньютона-Рафcона

;

;

, (4.31)

Дата добавления: 2013-12-12