Костина Л

BEGIN

Упражнение. Выполните приведенный алгоритм для деревьв

а) b)

1 7 1 7

8 2 3 2 8 3

5 5

6 6

4 4

Заметим, что в приведенном алгоритме, построенный им код определен однозначно.

Рассмотрим алгоритм восстановления дерево по его коду Прюфера i₁,…,i_n-2. Для этого

1. Восстановим заключительное звено дерева. Как было отмечено, им является ребра либо (i_n-2,n), в случае i_n-2¹n, либо ребро – (n,n-1), в случае i_n-2=n.

2. Для восстановления других ребер дерева выполним следующее

2.1 Пусть j=n-2.

2.2 Повторим n-2 раза

Если вершина i_j-1 (исключая j=1) еще не включена в дерево, то строим в нем ребро (i_j,i_j-1); в противном случае строим ребро (i_j,m), где m наибольший номер вершины еще не включенной в дерево.

Упражнение. Восстановите деревья по кодам Прюфера, полученным в предыдущем упражнении.

Замечание. Пусть задана произвольная последовательность натуральных чисел i₁,…,i_n-2, каждое из которых из промежутка 1..n. Тогда, по приведенному алгоритму, для этой последовательности может быть построено помеченное дерево, при этом двум разным последовательностям соответствуют два разных дерева.

Таким образом, теорема Кэли следует из установленной биекции.

Рассмотрим теперь задачу построения приведенных алгоритмов на языке Паскаль. Вначале разберем задачу построения кода Прюфера по заданному дереву. Будем считать, что дерево представлено в виде таблицы смежности, а его код Прюфера мы получаем в целочисленном массиве из n-2 элементов, где n – число вершин помеченного дерева.

Замечание. При решении многих задач, связанных с деревьями, выбранное для них представление не является наиболее удобным. В дальнейшем будут рассмотрены другие представления деревьев. В виде списка смежности, вообще говоря, может быть представлен граф самого общего вида, однако при решении данной задачи мы будем исходить из того, представленный в списке смежности граф действительно является деревом. Алгоритм проверки этого свойства представленного графа будет также рассмотрен ниже.

Для решения поставленной задачи мы будем исходить из того, что нам задан следующий глобальный контекст:

program pruff;

const n=7;

type v=^t;

t= record i:1..n; r:v end;

pru= array [0..n-2] of integer; {нулевой элемент – “корень”, равный n}

var k,i,j,a:integer; {n-1 – для основной программы }

sp: array [1..n] of v;

x,y: v;

Тогда процедура построения кода Прюфера выглядит так:

procedure inpruff(var pr:pru); {строит код Прюфера по списку смежности}

var rab:boolean;

begin

for j:=1 to n-2 do

begin k:=1;

В режиме неполного вычисления логических выражений оператор repeat можно заменить оператором while (sp[k]=nil) or (sp[k]^Ù.r<>nil) do k:=k+1;

repeat

rab:=false;

if sp[k]=nil then k:=k+1

else

if sp[k]^.r<>nil t hen k:=k+1

else rab:=true

until rab;

a:=sp[k]^.i; pr[j]:=a;

sp[k]:=nil;

x:=sp[a];

while (x^.i<>k) do begin y:=x; x:=x^.r end;

if sp[a]=x then sp[a]:=x^.r else y^.r:=x^.r

end;

end {inpruff};

Процедура восстановления дерева по коду Прюфера выглядит так:

procedure outpruff; {преобразует код Прюфера в список смежности }

procedure bk(var a,b:integer); {включить вершины a,b в список смежности}

begin new(x); new(y);

x^.i:=a; x^.r:=sp[b]; sp[b]:=x;

y^.i:=b; y^.r:=sp[a]; sp[a]:=y

end {bk};

begin { outpruff }

for i:=1 to n do sp[i]:=nil; pr[0]:=n;

a:=pr[n-2];

if a=n then i:=n-1 else i:=n; bk(a,i);

for j:=n-2 downto 1 do

{1} if sp[pr[j-1]]=nil then bk(pr[j-1],pr[j])

else begin while sp[i]<>nil do i:=i-1;

bk(i,pr[j])

end

end{outpruff};

Комментарий. Нулевой элемент в описании типа pru введен для корректного вычисления, в случае j=1, логического выражения в условии оператора {1}. В массиве pr, используемого процедурой outpruff в качестве значения кода Прюфера, нулевому элементу присвоено значение равное n.

Замечание. Код Прюфера является оптимальным по памяти кодирования деревьев. В самом деле, W =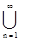W_n, где W_n – конечные множества. Предположим, что при каком-то способе кодирования элементов из W для запоминания одного элемента из W_n используется самое большое f(n) бит памяти. Кодирование f(n) называется оптимальным, если 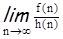=1, где h(n) = log₂ô W_nô.

Для оценки энтропия h(n) для множества деревьев с n вершинами по теореме Кэли имеем h(n) = (n-2)log₂n. Отсюда следует, что кодирование деревьев кодом Прюфера необходимо f(n) = (n-2)log₂n, бит памяти, и поэтому 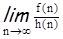=1.

При задании дерева списками смежности имеем 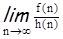=3 для неориентированных графов, и 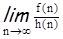=2 для ориентированных.

В. А. Евстигнеев. Применение теории графов в программировании. Наука. 1985.

Транспортная задача.

uses CRT; {1-туда 2-обратно 3-оба }

const n=8; mr=1.0E10;

type yk=^el;

el= record

nom: integer;

r: real;

tp: 1..3;

next: yk

end;

VAR sp: ARRAY[1..n] of record

b: real;

ref: yk

end;

f: TEXT;

i,j: integer;

a: real;

x,y: yk;

t:1..3;

procedure WWOD;

begin

Assign(f,'gro.txt');

Reset(f);

WHILE not EOF(f) DO begin

Read(f,i);

sp[i].b:=mr;

IF EOLN(f) then sp[i].ref:=NIL

else begin write(i);

Read(f,j,a,t);

New(x);

x^.nom:=j; x^.tp:=t;

x^.r:=a;

x^.next:=NIL;

sp[i].ref:=x;

WHILE not EOLN(f) DO

begin Read(f,j,a,t);

New(y);

y^.nom:=j;

y^.r:=a; y^.tp:=t;

y^.next:=NIL;

x^.next:=y;

x:=y

end

end

end

end;

procedure VYVOD;

var p:integer;

begin

WriteLn;

for p:=1 to n do begin

Write(p:3,' ',sp[p].b:9:1,' ');

x:=sp[p].ref;

while x <> NIL do begin

Write(x^.nom:2,x^.r:5:1,x^.tp:2,' ');

x:=x^.next

end;

WriteLn;

end;

end;

procedure WAVE (i: integer; rr: real);{ в ширину}

var pp,k: integer; p: array [1..n] of integer;

begin

x:=sp[i].ref;

pp:=0;

while x <> NIL do begin

k:=x^.nom;

a:=rr+x^.r;

if ((x^.tp=1)or(x^.tp=3)) and (sp[k].b>a) then begin

pp:=pp+1;

sp[k].b:=a;

p[pp]:=k

end;

x:=x^.next

end;

for k:=1 to pp do WAVE(p[k],sp[p[k]].b)

end;

{ PROCEDURE WAVE (i: INTEGER; rr: REAL);{в глубину}

VAR x:yk;

x:=sp[i].ref;

WHILE x <> NIL DO BEGIN

k:=x^.nom;

a:=rr+x^.r;

IF ((x^.tp=1)or(x^.tp=3)) and (sp[k].b>a) THEN

BEGIN sp[k].b:=a; WAVE(k,a) END;

x:=x^.next

END;

END;}

procedure REVERSE (j: integer);

var a: real;

k: integer;

begin

if j <> i then begin

x:=sp[j].ref;

k:=j;

a:=sp[j].b;

while x <> NIL do

begin

if (x^.tp>1) and (sp[x^.nom].b<a)

then begin k:=x^.nom; a:=sp[x^.nom].b end;

x:=x^.next;

end;

REVERSE(k);

Write('-->',j)

end

else Write(j)

end;

begin

ClrScr;

WWOD;

VYVOD;

Writeln('введите начальную и конечную вершины');

read(i,j);

sp[i].b:=0;

WAVE(i,0); VYVOD;

if sp[j].b>=mr then writeln('вершины не связаны путем')

else REVERSE(j)

end.

Костин В. А. 08.06.02

[1] Перманенты квадратных матриц является частным случаем перманентов прямоугольных матриц. Теория перманентов рассматривается в комбинаторной математике. Она имеет приложение к решению теоретико-вероятностных, комбинаторных и физических задач [3].

[2] Обработка информации, хранящейся в узлах бинарного дерева, по левостороннему обходу характеризуется тем, при обработки каждой вершины вначале совершается обход левой ветви, выходящей из этой вершины; затем обработка информация хранящейся непосредственно в этой вершине; после этого, обход правой ветви, исходящей из вершины.

К 90 Игровая терапия с тревожными детьми. 2003.-160 с. ISBN 5-9268-0158-3

- СПб.: Речь,

В книге рассматривается одна из самых актуальных проблем современной психологии — проблема детской тревожности. Автор подробным образом анали­зирует место игровой терапии в психокоррекционном процессе, детально опи­сывает приемы и методики проведения психокоррекционных занятий и необхо­димые материалы, приводит готовые программы игровой терапии.

Книга предназначена для психологов, педагогов, воспитателей, дефектологов, социальных работников, организаторов детского и семейного досуга, родителей.

© Л. М. Костина, 2001 © Издательство «Речь», 2003 ISBN 5-9268-0158-3 ® П. В. Борозспец (оформление), 2001

Дата добавления: 2013-12-11