Метод выбранных точек

Сглаживание результатов экспериментов

В случае невозможности обеспечения чистоты эксперимента, при получении табличных значений функции, нужно иметь в виду ошибки этих данных. Интерполирование усугубляет эти ошибки. В этом случае для аппроксимации прибегают к построению эмпирических формул, как моделей приближенных функциональных зависимостей. График эмпирических зависимостей не проходит через точки { x_i, y_i }. В результате экспериментальные данные как бы сглаживаются посредством подбора эмпирических формул.

Построение эмпирических формул состоит из 2-х этапов:

1) построение их общего вида;

2) определение наилучших значений содержащихся в них параметров.

1. Общий вид определяется из физических соображений. Если характер зависимостей неизвестен, то формулы выбираются произвольно, сообразуясь с их простотой. Сначала они выбираются из геометрических соображений среди простейших функций.

2. Если эмпирические формулы подобраны, то они представляются в общем виде:

y = j(x, a ₀, a ₁,..., a_m); (41)

j – известная функция; a_i – неизвестные коэффициенты, которые и подбираются для лучшего приближения.

Тогда отклонение (невязка) определяется:

e _i = j(x_i, a ₀, a ₁,..., a_m) – y_i; i = 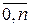. (42)

Задача нахождения a_i сводится к минимизации e _i. Существует несколько способов: метод выбранных точек, метод средних, метод наименьших квадратов.

В системе координат XOY наносится система точек и проводится простейшая плавная кривая или прямая. На проведенной прямой набирается система точек, число которых должно быть равно числу неизвестных коэффициентов в эмпирической формуле. Координаты (х ⁰ _j, y ⁰ _j) старательно измеряются и используются для записи условия прохождения через них прямой.

Из следующей системы находят a_i:

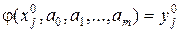; j = .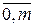

2.Метод средних

В данном случае параметры a_i для соотношения (41) находятся из условия:

. (43)

Условно равенство (43) разбивают на систему, состоящую из (m +1) уравнений:

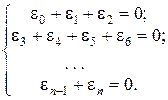(44)

Решают систему (44) и находят коэффициенты a_i.

Дата добавления: 2013-12-11