Параметрический стабилизатор переменного тока с дросселем насыщения

Параметрический стабилизатор на кремниевом стабилитроне

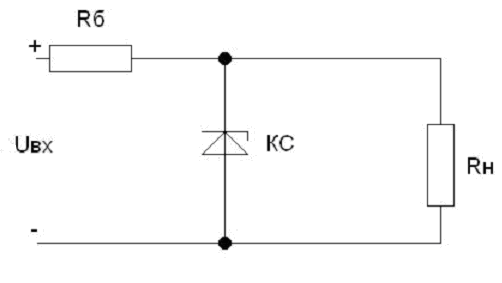
В этой схеме в качестве линейного элемента используется активное сопротивление R_б (балластное), а в качестве нелинейного – кремниевый стабилитрон, включенный в обратном направлении. Данная схема имеет низкий кпд и применяется для стабилизации только при небольших мощностях.

ВАХ кремниевого стабилитрона имеет следующий вид:

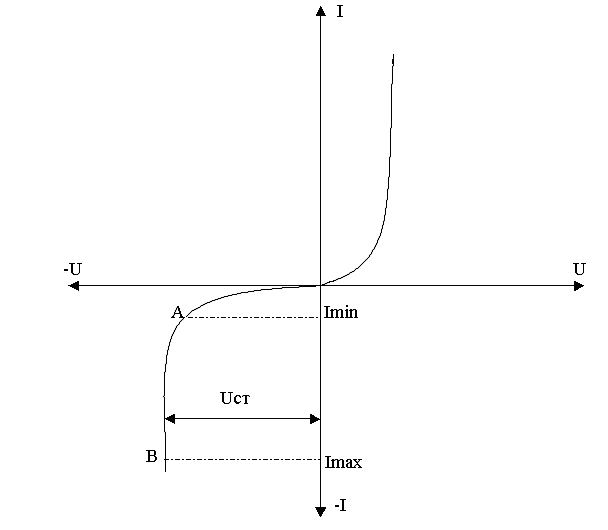
I_min – минимальный ток, при котором происходит стабилизация,

I_max – ток, при котором происходит тепловой пробой.

На практике для увеличения напряжения стабилизации часто включают последовательно несколько стабилитронов.

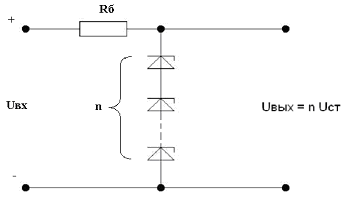
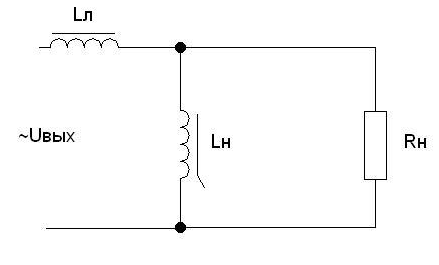
В данной схеме в качестве ЛЭ представлен дроссель L_л, сердечник которого работает в линейном режиме на линейной части петли гистерезиса. L_н – насыщенный нелинейный сердечник. ВАХ имеет точно такой же вид, как было рассмотрено выше в разделе «Принцип действия параметрического стабилизатора». Для того, чтобы дроссель был насыщен необходима значительная реактивная мощность, поэтому кпд и cosφ данной схемы будут невысокими. Чтобы устранить этот недостаток, параллельно L_н включают конденсатор С, в результате чего получается феррорезонансный стабилизатор.

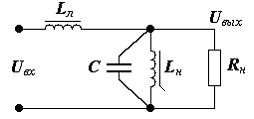
Где линейный элемент L_л, а нелинейный L_нС – феррорезонансный контур.

Рассмотрим векторную диаграмму при резонансе токов:

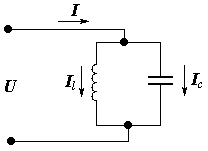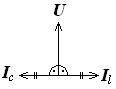I = I_l + I_c= 0, а сопротивление контура в точке резонанса Zк=U/ I=U/ 0=¥

Построим ВАХ феррорезонансного контура, учитывая характер токов в ветвях.

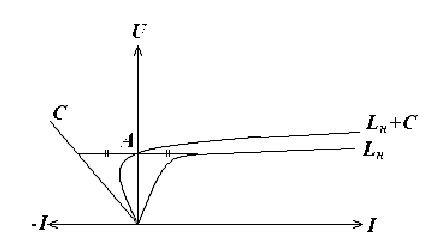
Характеристику контура получим складывая токи при одинаковых напряжениях.

Суммарная ВАХ имеет характерную точку А – точка феррорезонанса, при этом от сети ток не потребляется, а сердечник уже насыщен, т. е. проявляются нелинейные свойства элемента и происходит стабилизация.

Сопротивление контура при этом, учитывая потери, будет очень большим и активным, поэтому энергетические показатели (КПД и 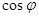) повышаются, по сравнению с первой схемой.

Недостатки данной схемы: малый коэффициент стабилизации т.к. ВАХ нелинейного элемента имеет некоторый подъём. Для устранения этого недостатка в стабилизатор вводится компенсационная обмотка (КО), и схема его имеет вид:

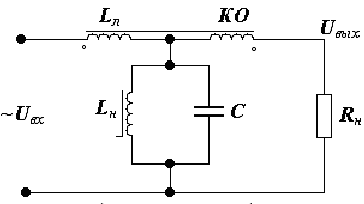
КО имеет небольшое количество витков W_ко и располагается на сердечнике линейного дросселя L_л. Она сфазирована так, что напряжение на ней будет находится в противофазе с напряжением на параллельном контуре.

Тогда:

U_вых = U_Lн+С - U_ко

Построим ВАХ КО:

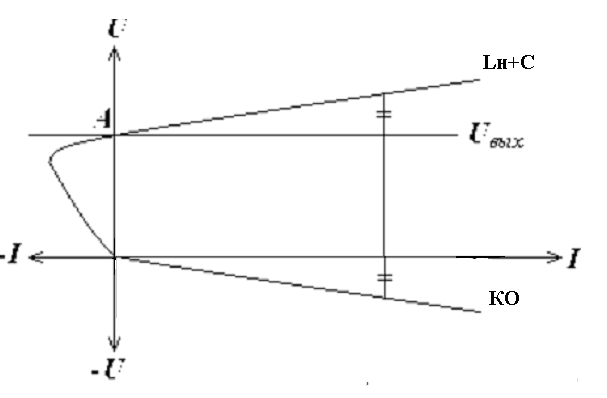
Если стабилизатор работает с неноминальным током, то произойдёт перекомпенсация, т.е. с увеличением U_вх напряжение U_вых будет уменьшаться. КО компенсирует только подъем ВАХ нелинейного элемента.

Дата добавления: 2013-12-12