Геометрический смысл матриц поворота

Прямая задача кинематики

Для систематического и обобщённого подхода к описанию и представлению расположения звеньев манипулятора (исполнительных механизмов робота) относительно заданной абсолютной системы координат применяют матричную и векторную алгебру.

Звенья манипулятора могут совершать вращательное и/или поступательное движение относительно абсолютной системы координат, оси которой параллельны осям сочленений звеньев. Прямая задача кинематики сводится к определению матрицы преобразования, устанавливающей связь между абсолютной и связанной системами координат. Для описания вращательного движения связанной системы отсчёта относительно абсолютной используется матрица поворота (вращения) размерностью 3´3. Для учёта поступательного движения используется матрица однородного преобразования размерностью 4´4.

Матрицы поворота (вращения).

Матрицу поворота размерностью 3´3 можно определить как матрицу преобразования трёхмерного вектора положения в евклидовом пространстве, переводящую его из повернутой (связанной) системы отсчёта OUVW в абсолютную систему координат OXYZ. На рис.2.2 показаны две правые прямоугольные системы координат: система координат OXYZ с осями OX, OY, OZ и система OUVW с осями OU, OV, OW. Начала этих систем совпадают и расположены в точке О.

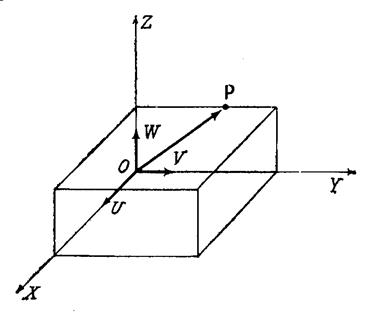
Рисунок 2.2. Абсолютная и связанная системы координат

Система OXYZ фиксирована в трёхмерном пространстве и принята за абсолютную. Система координат OUVW вращается относительно абсолютной и физически рассматривается как связанная система координат. Это означает, что она жёстко связанна с твёрдым телом (например, самолётом) и движется вместе с ним.

Пусть (i_x, j_y, k_z) и (i_u, j_v, k_w) – единичные векторы, направленные вдоль своей системы OXYZ и OUVW соответственно. Некоторую точку P в пространстве можно характеризовать координатами относительно любой из указанных систем:

p _uvw = (p_u, p_v, p_w) ^T и p _xyz = (p_x, p_y, p_z) ^T (2-1)

где T - означает операцию транспонирования.

Задача состоит в том, чтобы определить матрицу R размерностью 3´3, которая преобразует координаты p _uvw в координаты вектора p системе OXYZ после того, как система OUVW будет повёрнута, т.е.:

p _xyz = Rp _uvw. (2-2)

Заметим, что физически точка p вращается вместе с системой координат OUVW.

Из определения компонент вектора имеем:

p _uvw = p_u × i _u+p_v × j _v+p_w ×k _w, (2-3)

где p_u, p_v, и p_w представляют собой составляющие вектора p вдоль осей OU, ОV, ОW соответственно, или проекции вектора p на эти оси. Используя определение скалярного произведения и равенства (2-3), получаем:

p_x = i _x × p = i _x × i _u × p_u + i _x × j _v × p_v + i _x × k _w × p_w,

p_y = j _y × p = i _y × i _u × p_u + j _y × j _v × p_v + j _y × k _w × p_w,

p_z = k _z × p = k _z × i _u × p_u + k _z × j _v × p_v + k _z × k _w × p_w. (2-4)

или в матричной форме:

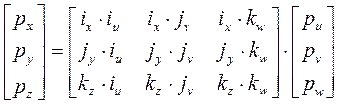. (2-5)

С учётом этого выражения матрица R в равенстве (2-2) примет вид:

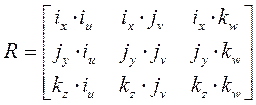. (2-6)

Аналогично, координаты p _uvw можно получить из координат p _xyz:

p _uvw = Q × p _xyz, (2-7)

или

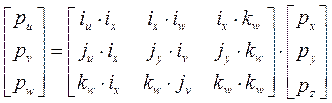. (2-8)

Поскольку операция скалярного произведения коммутативна, то из соотношений (2-6)…(2-8) следует

Q = R ^-1 = R ^T, (2-9)

QR = R ^T R = R ^-1 × R = I ₃, (2-10)

где I₃ – единичная матрица размерностью 3´3.

Преобразование, определяемое формулой (2-9) или (2-10), называется ортогональным преобразованием.

Особый интерес представляет матрица поворота системы OUVW относительно каждой из трёх основных системы OXYZ. Если положение системы OUVW в пространстве изменяется за счёт поворота этой системы на угол a вокруг оси OX, то в системе отсчёта OXYZ изменяются и координаты (p_x, p_y, p_z) ^T точки (p_u, p_v, p_w). Соответствующая матрица преобразования R_x,a называется матрицей поворота вокруг оси OX на угол a. Основываясь на полученных выше результатах, для матрицы R _x,a имеем:

p _xyz = R _x,a × p _uvw, (2-11)

причём i _x 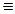i _u, и

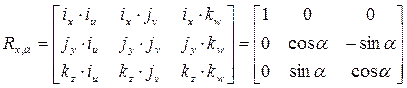. (2-12)

Аналогично, трёхмерные (размерностью 3´3) матрицы поворота вокруг оси OY на угол j и вокруг оси OZ на угол q имеют соответственно вид (рис.2.3).

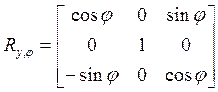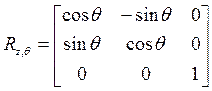, . (2-13)

Матрицы R _x,a, R _y,j и R _z,q называют матрицами элементарных поворотов.

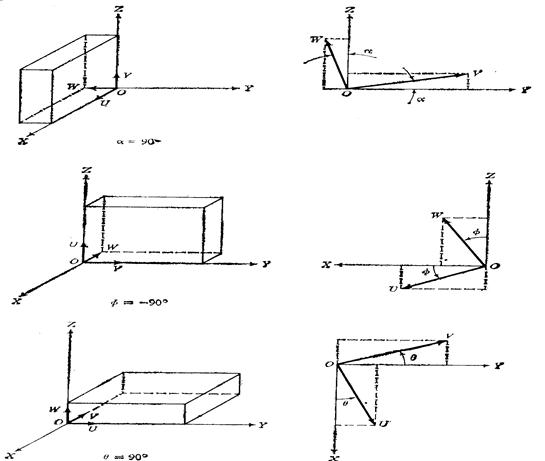
Рисунок 2.3. Вращающаяся система координат

Пусть точка p в системе отсчёта OUVW имеет координаты (1, 0, 0), т. е. p _uvw = i _u. Тогда первый столбец матрицы поворота представляет собой координаты этой точки относительно системы отсчёта OXYZ. Аналогично, выбирая в качестве p векторы (0, 1, 0) ^Т и (0, 0, 1) ^Т, легко видеть, что второй и третий столбцы матрицы поворота представляют собой координаты единичных векторов в направлении осей OV и OW системы OUVW относительно системы отсчёта OXYZ.

Таким образом, если заданы абсолютная система отсчёта OXYZ и матрица поворота, то векторы-столбцы этой матрицы задают в системе OXYZ координаты единичных векторов в направлении основных осей системы OUVW. Это позволяет определить положение осей системы координат OUVW относительно абсолютной системы координат. Таким образом, матрица поворота определяет положение основных осей повёрнутой системы координат относительно абсолютной системы координат.

Поскольку операция обращения матрицы поворота совпадает с операцией транспонирования, то векторы – строки матрицы поворота задают направление основных осей абсолютной системы координат OXYZ в повёрнутой системе координат OUVW.

Такая геометрическая интерпретация матрицы поворота даёт ключ к решению многих задач кинематики манипулятора.

Дата добавления: 2013-12-12