Звенья, сочленения и их параметры

Лекция 3

Механический манипулятор состоит из звеньев, соединенных вращательными или поступательными сочленениями (рис. 3.1). Каждая пара, состоящая из звена и сочленения, обеспечивает одну степень свободы. Следовательно, манипулятор с N степенями свободы содержит N пар «звено-шарнир». Звено 0 соединено с основанием, где обычно размещается инерциальная система координат динамической системы, а последнее звено снабжено рабочим инструментом.

Звенья и сочленения нумеруются по возрастанию от стойки к схвату манипулятора. Каждое звено соединено не более чем с двумя другими так, чтобы не образовывалось замкнутых цепей.

В общем случае два звена соединяются элементарным сочленением, имеющим две соприкасающиеся поверхности, скользящие друг относительно друга.

в манипуляторах обычно используются только вращательные и поступательные. В месте соединения двух звеньев определяется ось i- го сочленения (рис. 5.3). Эта ось имеет две пересекающие ее нормали, каждая из которых соответствует одному из звеньев (звена i -1 и звена i), определяется величиной d_i – расстоянием между этими нормалями, отсчитываемым вдоль оси сочленения.

Рисунок 5.2. Элементарные сочленения

Присоединенный угол Q_i между нормалями измеряется в плоскости, перпендикулярной оси сочленения. Таким образом, d_i и Q_i можно назвать расстоянием и углом между смежными звеньями. Они определяют относительное положение соседних звеньев.

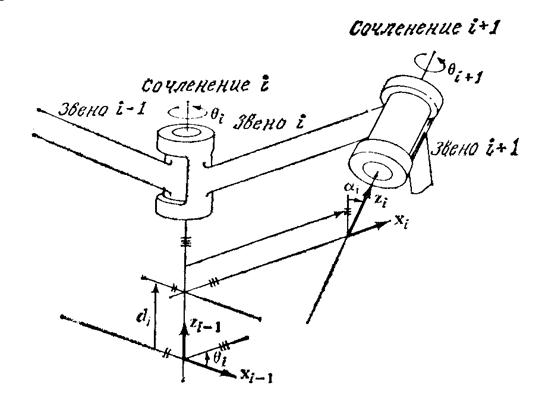
Рисунок 5.3. Система координат и ее параметры

Звено i (i =1, 2, 3, …., 6) соединено не более чем с двумя звеньями (i -1-м и i +1-м звеньями). Таким образом, в точках соединения i -го звена с двумя соседними определены две оси сочленения. Важное свойство звеньев с точки зрения кинематики состоит в том, что они сохраняют неизменной конфигурацию относительного расположения соседних сочленений, характеризуемую параметрами a_i и _i. В качестве параметра a_i выбрано кратчайшее расстояние между осями z_i-1 и z_i i -го и i+1- го сочленений соответственно, измеряемое вдоль их общей нормали. Угол _i – угол между осями сочленений, измеряемый в плоскости, перпендикулярной их общей нормали. Таким образом, a_i и можно рассматривать соответственно как длину и угол скрутки i –го звена. Эти параметры характеризуют конструктивные особенности i –го звена.

Итак, с каждым звеном манипулятора связаны четыре параметра: a_i, α_i d_i, Q_i. Если для этих параметров установить правило выбора знаков, то они составят набор, достаточный для описания кинематической схемы каждого звена манипулятора. Эти параметры можно разделить на две пары: параметры звена (a_i, α_i), которые характеризуют конструкцию звена, и параметры сочленения (d_i, Q_i), характеризующие относительное положение соседних звеньев.

Дата добавления: 2013-12-12