Уравнения кинематики манипулятора

Лекция 4

Для манипулятора Пума

Рисунок 3.4. Формирование систем координат звеньев

После построения ДХ-координат для всех звеньев можно построить однородные матрицы преобразования, связывающие i- ю и (i -1)-ю системы координат:

^i-1 A _i = T _z,d T _z,Q T _x,a T _x,α =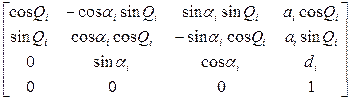. (3-1)

Преобразуя (3-1), найдем, что матрица, обратная к ^i-1 А _i, имеет вид:

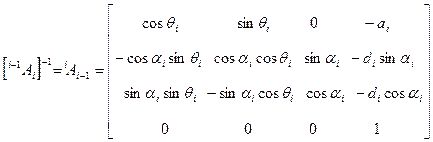. (3.2)

где - константы, а - присоединенная переменная, если рассматриваемое сочленение – вращательное.

Используя матрицу 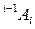, можно связать однородные координаты р _i точки р относительно i -й системы координат (точка р покоится в i –й системе координат)с односторонними координатами этой точки относительно (i -1)-й системы тсчета, связанной с (i -1)-м звеном. Эта связь устанавливается равенством:

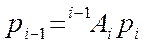, (3-3)

где 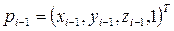и .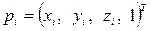

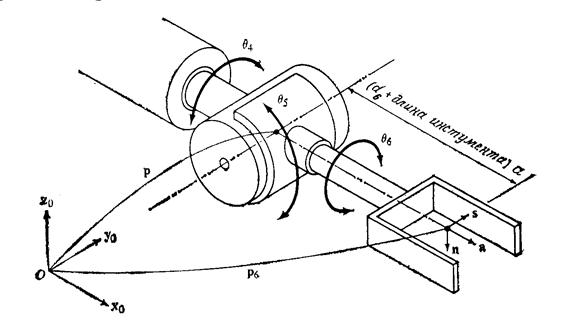
Рисунок 4.1. Система координат схватa

Однородная матрица 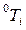, определяющая положение i -й системы координат относительно базовой системы координат, представляет собой произведение последовательности однородных матриц преобразования ^i-1A_i и имеет вид:

⁰ T _i = ⁰A _i ¹A _i …^i-1A _i =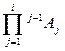==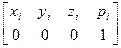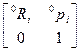для i =1, 2, …, n,

где 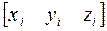- матрица, определяющая ориентацию i -й системы координат, связанной с i -м звеном, по отношению к базовой системе координат. Это верхняя левая подматрица , имеющая размерность 3×3.

р _i - вектор, соединяющий начало базовой системы координат с началом i -й системы координат. Это верхняя правая подматрица матрицы , имеющая размерность 3×1. В частности, при i =6 мы получаем матрицу 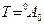, которая задает положение и ориентацию схвата манипулятора относительно базовой системы координат. Эта матрица часто используется при описании кинематики манипулятора. Ее называют «матрицей манипулятора».

Положим, что матрица Т имеет следующий вид:

T ====,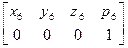

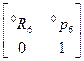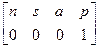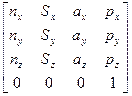где n – вектор нормали к схвату. В случае плоскопараллельного движения пальцев этот вектор перпендикулярен пальцам манипулятора;

s – касательный вектор схвата. Он лежит в плоскости движения пальцев и указывает направление движения пальцев во время открытия или закрытия схвата;

a - вектор подхода схвата. Он направлен по нормали к ладони схвата, (т.е. перпендикулярно плоскости крепления инструмента в схвате);

p - вектор положения схвата. Этот вектор направлен из начала базовой системы координат к началу системы координат схвата, которое, как правило, расположено в точке, являющейся геометрическим центром полностью сжатых пальцев.

Если положение манипулятора в абсолютном пространстве определяется матрицей B, а в схвате манипулятора зафиксирован инструмент, положение которого в системе координат схвата определяется матрицей H, то положение рабочего узла инструмента относительно абсолютной системы координат дается произведением матриц В, ⁰ Т ₀ и Н, т.е.:

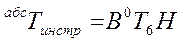. (4-1)

При этом H ≡ 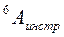, B ≡ .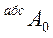

Решение прямой задачи кинематики для шестизвенного манипулятора является вычислением T =⁰ A ₆ с помощью последовательного перемножения шести матриц ^{i -1} A _{i .} Решение этой задачи приводит к единственной матрице Т при заданных 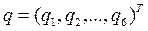и фиксированных системах координат, где 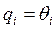для вращательного сочленения и 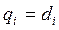для поступательного сочленения. Ограничения определяются только физическими пределами изменения 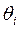для каждого сочленения манипулятора.

Матрица T манипулятора Пума имеет вид:

T = ⁰ A ₁¹ A ₂² A ₃³ A ₄⁴ A ₅⁵ A ₆=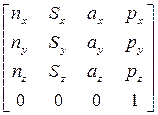, (4-2)

Рассмотрим произвольную точку, неподвижную относительно i -го звена и заданную в системе координат i -го звена однородными координатами 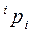(рис. 4.2):

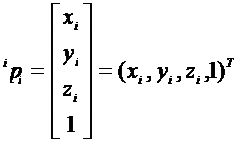. (4-3)

Обозначим через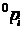 координаты этой же точки относительно базовой системы координат. Матрица 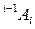обозначает матрицу преобразования однородных координат, определяющую пространственное положение системы координат i -го звена относительно системы координат (i -1)-го звена, а 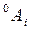-матрицу, определяющую связь между системой координат i -го звена и базовой системой координат.

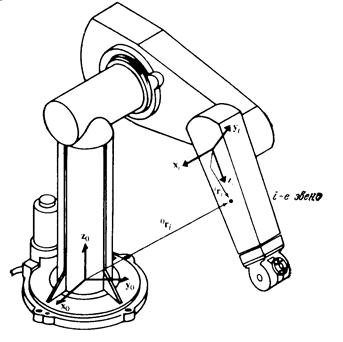
Рисунок 4.2. Точка 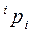i -го звена

Тогда связь между 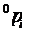и 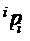определяется соотношением:

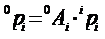, (4-4)

где .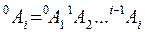

(4-5)

Дата добавления: 2013-12-12