Геометрический подход

Обратная задача кинематики

В этом разделе рассматривается обратная задача кинематики шестизвенного манипулятора. Необходимо по заданной матрице ⁰ T ₆ положения и ориентации схвата шестизвенного манипулятора и известным параметрам его звеньев и сочленений определить присоединенные параметры 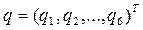манипулятора, обеспечивающие заданное положение схвата.

Для того, чтобы решение обратной задачи кинематики было получено в явном виде, необходимо, чтобы конструкция робота удовлетворяла одному из двух условий:

1. Оси трех смежных сочленений пересекаются в одной точке.

2. Оси трех смежных сочленений параллельны между собой.

Из равенства (4-7) видно, что матрица T является функцией синусов и косинусов углов 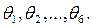Приравнивая элементы матриц в левой и правой частях матричного уравнения (4-7), получаем, например, для манипулятора Пума двенадцать уравнений (4-3) – (4-6) относительно шести неизвестных (присоединенных углов). Поскольку число уравнений превышает число переменных, можно сразу сделать вывод о том, что решение обратной задачи кинематики для манипулятора Пума не единственно. Мы рассмотрим два метода решения обратной задачи кинематики: метод обратных преобразований в эйлеровых координатах и геометрический подход, выгодно отличающийся наглядностью.

В этом разделе излагается геометрический подход к решению обратной задачи кинематики шестизвенного манипулятора с вращательными сочленениями типа Пума.

По аналогии с геометрией человеческой руки и в соответствии с расположением систем координат звеньев различные конфигурации манипулятора Пума определяются с помощью трех индикаторов конфигурации (РУКА, ЛОКОТЬ, ЗАПЯСТЬЕ). Два индикатора характеризуют взаимное расположение первых трех сочленений, а третий – расположение последних трех. Для шестиосных манипуляторов типа Пума существуют четыре различных решения обратной задачи кинематики первых трех сочленений и каждому из этих четырех решений соответствует по два допустимых решения для последних трех сочленений.

Решение производится в два этапа.

I этап. Cначала вычисляется вектор, направленный от плеча к запястью. Проекции этого вектора на плоскость x _{i -1} y _{i -1} используются при нахождении присоединенного угла i -го сочленения (i =1, 2, 3) для первых трех сочленений.

II этап. Использование предыдущего решения для решения последних трех сочленений, подматрицы поворота матриц ⁰ Т и ^{i -1} A _i (i =4, 5, 6) и проекции систем координат звеньев на плоскость x _{i -1} y _{i -1}.

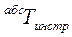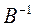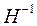Если задана матрица , то, умножив эту матрицу слева и справа на и соответственно, можно вычислить 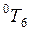и затем, воспользовавшись указанным способом, получить:

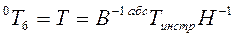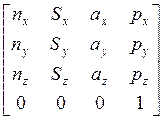=. (4-1)

Дата добавления: 2013-12-12