Динамика манипулятора

Лекция 5

Предметом динамики манипулятора как раздела робототехники является математическое описание действующих на манипулятор сил и моментов в форме уравнений динамики движения. Также уравнения необходимы для моделирования движения манипулятора с помощью ЭВМ, при выборе законов уравнения и при оценке качества кинематической схемы и конструкции манипулятора.

Задача управления включает задачу формирования динамической модели реального манипулятора и задачу выбора законов или стратегий управления, обеспечивающих выполнение поставленных целей.

Динамическая модель манипулятора может быть построена на основе использования известных законов ньютоновой или лагранжевой механики. Результатом применения этих законов является уравнения, связывающие действующие в сочленениях силы и моменты с кинематическими характеристиками и параметрами движения звеньев.

Таким образом, уравнения динамики движения реального манипулятора могут быть получены методами Лагранжа-Эйлера или Ньютона-Эйлера. Уравнения Лагранжа-Эйлера обеспечивают строгое описание динамики манипулятора. Их можно использовать для решения прямой и обратной задачи динамики.

Прямая задача состоит в том, чтобы по заданным силам и моментам определить обобщённые ускорения, интегрирование которых позволит получить значения обобщённых координат и скоростей.

Обратная задача динамики заключается в том, чтобы по заданным обобщённым координатам, скоростям и ускорениям определить действующие в сочленениях манипулятора силы и моменты.

Для решения обеих задач, как правило, необходимо вычислить динамические коэффициенты 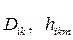и 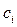. Вычисление этих коэффициентов требует выполнения очень большого числа арифметических операций. В связи с этим уравнения Лагранжа-Эйлера без дополнительных упрощений практически неприменимы для управления манипулятором в реальном времени.

С целью получения более эффективных с вычислительной точки зрения алгоритмов расчёта обобщённых сил и моментов используют уравнения Ньютона-Эйлера, которые просты по содержанию, но весьма трудоёмки. Результатом является система прямых и обратных рекуррентных уравнений, последовательно применяемых к звеньям манипулятора. Это позволяет реализовать простые законы управлением манипулятора в реальном времени.

Дата добавления: 2013-12-12