
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В физической лаборатории
|
|
|
|
Введение
Работа в физической лаборатории требует вдумчивого, упорного и ответственного отношения. Она связана не только с умением правильного обращения с измерительными приборами, но и с правильной и осознанной обработкой результатов измерений. Настоящее учебное пособие курс посвящено вопросам обработки результатов измерений при выполнении работ в лабораториях физического практикума. Он ориентирован на студентов, профессиональное образовательные программы которых предусматривают выполнение лабораторных работ в рамках изучения физики. Учебное пособие может быть полезным и учителям при подготовке физического практикума в школе.
Кроме обработки результатов измерений студенты должны научиться правильно записывать эти результаты, заполнять таблицы, грамотно рисовать графики и оформлять отчеты по лабораторным работам. Перечисленные вопросы также рассматриваются в данном пособии.
В конце пособия приведен список литературы, которая использовалась при его написании. Изучение её можно рекомендовать тем, кто желает углубить знания по рассматриваемым здесь вопросам.
§1. Измерения физических величин
1.1. Понятия об измерениях физической величины
Физика – наука экспериментальная: её законы базируются на экспериментальных фактах, установленных или подтвержденных опытным путем. Поэтому работа в физических лабораториях является необходимой и важной частью изучения законов физики. Одной из целей эксперимента является поиск таких параметров физических явлений, которые можно измерить. Свойства физических объектов, которые можно измерить, называют физическими величинами.
Под измерением понимают нахождение значения физической величины опытным путем с помощью специальных технических средств. При этом значение физической величины G сравнивают с единицей измерения [ G ]. Число, которое получается при измерениях, называют численным значением { G } физической величины:
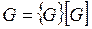 (1.1)
(1.1)
Таким образом, значение любой физической величины равно произведению численного значения на единицу измерения.
Различают прямые и косвенные измерения. Прямым измерением называют измерение, при котором искомое значение физической величины находят непосредственно из опытных данных. Например: измерение массы на циферблатных или равноплечных весах, температуры термометром, длины с помощью линейки. Косвенным измерением называют измерение, при котором искомое значение физической величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Например: нахождение плотности однородного тела по его массе и объёму (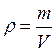 ), нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения (
), нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения (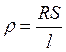 ).
).
Измерения, при которых число опытов равно числу измеряемых величин, называют однократными. Если число опытов превышает число измеряемых величин, то такие измерения называют многократными.
Многие измерительные приборы снабжены измерительными шкалами. Введем ряд понятий, которые их характеризуют:
- отметкой шкалы называют знак, соответствующий некоторому значению измеряемой физической величины;
- делением шкалы называют промежуток между двумя соседними отметками шкалы;
- ценой деления шкалы называют разность значений физической величины, соответствующих двум соседним отметкам шкалы.
При измерении физических величин используют различные меры. Мерой называют средства измерений, предназначенные для воспроизведений физической величины заданного размера. Например: гиря – мера массы; измерительный резистор – мера электрического сопротивления; температурная лампа – мера яркостной температуры; кварцевый генератор – мера частоты электрических колебаний. Номинальным значением меры называют значение физической величины, указанное на мере или приписанное ей.
1.2. Системы единиц физических величин
В принципе, единицы измерения всех физических величин можно установить произвольно и независимо друг от друга. Но это очень неудобно на практике. Поэтому, независимо устанавливается несколько единиц физических величин. Эти величины и их единицы называют основными. Остальные единицы устанавливают через основные посредством физических законов и определений. Такие единицы называют производными.
Совокупность основных и производных единиц, относящихся к некоторой системе физических величин и построенной в соответствии с принятыми принципами, образуют систему единиц.
Принципы установления произвольных величин:
1) Выбрать величины, единицы которых принять за основные.
2) Установить размер (эталон) этих единиц.
3) Выбрать определяющие уравнения, связывающие основные и производные единицы и приравнять их единице коэффициентом пропорциональности.
В физике имеется 7 основных единиц измерения: для длины, массы, времени, температуры, количества вещества, силы тока, силы света.
Для основных единиц СИ приняты следующие обозначения их размерности (размерностью физической величины называется выражение, характеризующее связь этой физической величины с основными величинами данной системы единиц) и единицы измерения: длина – L (1 метр), время – T (1 секунда), масса – M (1 килограмм), температура – Θ (1 кельвин), количество вещества – N (1 моль), сила тока – I (1 ампер), сила света – J (1 кандела).
К эталонам основных единиц предъявляются следующие требования:
1) Сохранение постоянства размера.
2) Воспроизводимость.
3) Возможность восстановления в случае утери.
4) Возможность сравнения эталонов в различных местах.
Международная система единиц (СИ – система интернациональная) принята на ХI Генеральной конференции по мерам и весам в 1960г. В СССР в качестве обязательной СИ введена в 1982г. (ГОСТ 8.417-81). Стандарт распространяется на все области науки и техники, но в научных исследованиях временно могут допускаться другие системы единиц (СГС, Гауссова, естественные системы).
§2. Погрешности измерений и их классификация
Истинным значением физической величины называют такое её значение, которое идеальным образом отражало бы в качественном или количественном отношении существующее свойство объекта. При измерении любой физической величины её истинное значение определить невозможно: повторные измерения одной и той же физической величины дают результаты, отличающиеся друг от друга даже тогда, когда они проводились одним и тем же лицом, одним и тем же способом, посредством одних и тех же приборов. Причина этого заключается как в ограниченной точности приборов, так и во влиянии на измерение многих факторов, учесть которые невозможно. Поэтому любые измерения всегда производятся с погрешностями (наряду с термином «погрешность» используется также слово «ошибка» в значении именно погрешность, а не какое-то ошибочное действие). Погрешностью измерения называют отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерения, выраженная в единицах измеряемой величины, называется абсолютной погрешностью измерения. Абсолютная погрешность измерения в принципе определяется формулой:
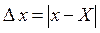 , (2.1)
, (2.1)
где x – результат измерения (оценка измеряемой величины в виде некоторого числа принятых для неё единиц, полученная путем измерения), X – истинное значение физической величины.
Качество измерения определяет относительная погрешность – отношение абсолютной погрешности измерения к модулю истинного значения измеряемой величины:
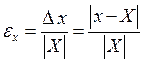 . (2.2)
. (2.2)
Относительная погрешность может быть выражена в процентах, при этом она определяется по формуле
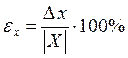 . (2.3)
. (2.3)
Качество измерений, отражающее близость результатов к истинному значению измеряемой величины, определяется также точностью измерений. Высокая точность измерения соответствует малым погрешностям. Количественно точность может быть выражена величиной, обратной относительной погрешности, определяемой по формуле (2.2).
Поскольку истинное значение остается неизвестным, на практике можно найти лишь приближенную оценку погрешностей измерения.
В зависимости от источников погрешностей различают следующие составляющие погрешностей измерений:
а. Методическая погрешность ΔМ, которая возникает вследствие несовершенства метода измерений, который обусловлен отличием реальной процедуры измерения от выбранной идеализированной модели измерения.
б. Погрешность прибора ΔП, которая обусловлена тем, что показание любого, даже самого точного прибора всегда отличаются от истинного значения измеряемой величины. Погрешность прибора может содержать случайную и систематическую составляющие (см. далее в данном параграфе).
в. Погрешность округления ΔО, возникающая при считывании со шкалы прибора результата измерения, который всегда содержит конечное число значащих цифр, т.е. всегда имеет погрешность округления. Значащими цифрами числа называют все его цифры, начиная с первой, отличной от нуля слева. Например: число 0,00707 содержит три значащие цифры; число 2,500 – четыре значащие цифры.
г. Погрешность вычисления ΔВ, которая появляется в процессе математической обработки результатов измерений, когда вычисления ведутся с конечным числом значащих цифр и при этом возникают погрешности, связанные с такими вычислениями.
д. Промахи – погрешности, существенно превышающие ожидаемые значения погрешностей при данных условиях эксперимента. Промахи могут быть вызваны невнимательностью экспериментатора, неправильно сделавшего отсчет или неверно записавшего его, неисправностью средств измерения, резким сотрясением установки, наводками при коротком замыкании цепи соседней установки и т.п. Промахи должны быть исключены из результатов измерений. Такое исключение осуществляется по специальной методике, которая будет изложена ниже (см. раздел 3.5).
По характеру проявления различают случайные и систематические погрешности. Систематической называют составляющую погрешности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Например: погрешность от несоответствия действительного значения меры, с помощью которой выполняют измерение, ее номинальному значению; погрешность, возникающая при измерении объема жидкости без учета теплового расширения в случае изменения температуры; погрешность при изменении массы, если не учитывать действия выталкивающей силы воздуха на взвешиваемое тело и на разновесах; шкала линейки может быть нанесена неравномерно, положение нуля термометра может не соответствовать нулевой температуре, капилляр термометра в разных местах может иметь разное сечение – эти причины также приводят к систематическим погрешностям. Систематическую погрешность вносит также округление численных значение физических констант.
Поскольку причины, вызывающие систематические погрешности в большинстве случаев известны, то эти погрешности, в принципе, могут быть исключены или значительно уменьшены за счет изменения метода измерения, введения поправок к показаниям приборов, учёта систематического влияния внешних факторов, использованием в расчётах более точных значений физических констант и т.д. Однако на практике этого не всегда легко добиться, поскольку повторные измерения не выявляют систематических погрешностей.
Случайной называют составляющую погрешности измерения, изменяющуюся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются сложной совокупностью причин, трудно поддающихся анализу. Присутствие случайных погрешностей (в отличие от систематических) легко обнаруживаются при повторных измерениях в виде некоторого разброса получаемых результатов. В качестве примера случайных погрешностей можно привести погрешность вследствие вариации показаний измерительного прибора; погрешность округления при отсчитывании показаний измерительного прибора; погрешность вследствие параллакса, которая может возникать при снятии показаний стрелочных приборов. Случайные погрешности вызываются также сотрясениями фундамента здания, влиянием незначительного движения воздуха, колебаниями напряжения в сети, питающей приборы, и т.д.
Главной отличительной чертой случайных погрешностей является их непредсказуемость от одного отсчета к другому. Поэтому оценка случайных погрешностей может быть осуществлена только на основе теории вероятностей и математической статистики. Далее будет показано, что случайная погрешность уменьшается при увеличении числа измерений физической величины. Однако, случайные ошибки надо сравнивать с систематическими, так как иначе может оказаться, что повышение точности измерений будет иллюзорным.
В качестве наглядной иллюстрации вышесказанного на Рис. 1а на числовой оси приведены результаты пяти измерений, отмеченных чёрточками, а также истинное значение X измеряемой величины, когда имеются только случайные ошибки или случайные ошибки значительно превышают систематические; на Рис. 1б представлены результаты пяти измерений, когда при наличии случайных ошибок систематические вносят значительный вклад.

§3. Статистический анализ случайных погрешностей
При выполнении многократных измерений необходим метод, который позволил бы обрабатывать полученные результаты. Одним из удобных методов является использование распределения. Предельным распределением (при бесконечном количестве измерений) результатов эксперимента является распределение Гаусса (отметим, что оно не является единственно возможным).
Вопросу обоснования применимости распределения Гаусса в теории ошибок в литературе уделяется много внимания. Но лучше всего, касаясь этого вопроса, пожалуй, сказал тот, кто сказал «экспериментаторы верят в него, полагаясь на доказательства математиков, а математики – полагаясь на экспериментальное обоснование». Тем не менее, распределение Гаусса можно в какой-то мере обосновать.
3.1. Предельное распределение
Результаты серии измерений одной величины можно наглядно представить, построив диаграмму, которая показала бы, как часто получены те или иные значения. Такая диаграмма называется гистограммой.
Вначале рассмотрим измерение величины, которая может принимать дискретные значения. Пусть, например, выполняется подсчет частиц, которые регистрируются счетчиком за одну минуту. Будем считать, что выполнено десять измерений и получены следующие результаты: 56, 59, 54, 58, 56, 57, 56, 58, 57, 57. Эти результаты удобно записать в виде следующей таблицы, располагая их по мере возрастания значения.
Таблица 1
| Значения хk | ||||||
| Число реализаций nk |
Полученные результаты позволяют вычислить среднее значение регистрируемых за одну минуту частиц:
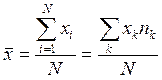 , (3.1.1)
, (3.1.1)
где N – число измерений. Величину, определяющую долю от полного числа измерений, в которой реализуется результат xк принято называть частотой:
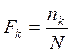 . (3.1.2)
. (3.1.2)
При этом среднее значение можно определить по формуле:
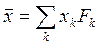 . (3.1.3)
. (3.1.3)
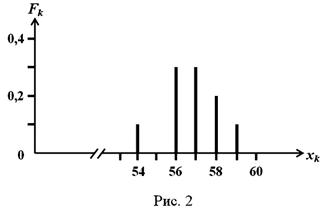 Частоты Fk характеризуют распределение результатов измерения в виде гистограмм, на которых по вертикальной оси откладывают значения Fk, а по горизонтальной – xk.
Частоты Fk характеризуют распределение результатов измерения в виде гистограмм, на которых по вертикальной оси откладывают значения Fk, а по горизонтальной – xk.
Если сложить частоты всех возможных значений xk, то в результате получается единица
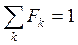 . (3.1.4)
. (3.1.4)
Это условие называют условием нормировки.
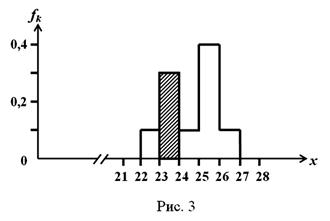 Гистограмма, представленная на Рис. 2, определяет распределение дискретной величины. Вместе с этим, зачастую встречаются физические величины, имеющие непрерывный диапазон возможных значений. Например, при измерении расстояния между двумя точками с помощью линейки с ценой деления 1 мм, могут быть получены следующие результаты (в сантиметрах): 26,4; 23,9; 25,1; 24,6; 22,7; 23,8; 25,2; 23,7; 25,3; 25,4. Если по полученным результатам построить гистограмму, подобную предыдущей, то она будет содержать десять черточек одинаковой высоты и являться малоинформативной. Поэтому диапазон возможных значений разбивают на интервалы и подсчитывают, какое количество измерений попадает в каждый интервал. Выбирая интервал в размере Δ k =1,0 см, можно построить представленную на Рис. 3 гистограмму для непрерывной функции. Причем для непрерывной величины площадь fk ·Δ k к-го прямоугольника (на Рис. 3 он заштрихован) имеет такой же смысл, что и высота к-той черточки Fk в случае гистограммы для дискретной величины (см. Рис. 2).
Гистограмма, представленная на Рис. 2, определяет распределение дискретной величины. Вместе с этим, зачастую встречаются физические величины, имеющие непрерывный диапазон возможных значений. Например, при измерении расстояния между двумя точками с помощью линейки с ценой деления 1 мм, могут быть получены следующие результаты (в сантиметрах): 26,4; 23,9; 25,1; 24,6; 22,7; 23,8; 25,2; 23,7; 25,3; 25,4. Если по полученным результатам построить гистограмму, подобную предыдущей, то она будет содержать десять черточек одинаковой высоты и являться малоинформативной. Поэтому диапазон возможных значений разбивают на интервалы и подсчитывают, какое количество измерений попадает в каждый интервал. Выбирая интервал в размере Δ k =1,0 см, можно построить представленную на Рис. 3 гистограмму для непрерывной функции. Причем для непрерывной величины площадь fk ·Δ k к-го прямоугольника (на Рис. 3 он заштрихован) имеет такой же смысл, что и высота к-той черточки Fk в случае гистограммы для дискретной величины (см. Рис. 2).
При увеличении числа измерений N можно уменьшить ширину интервала Δ k. Так на Рис. 4а представлена гистограмма в случае ста измерений того же расстояния x при Δ k =1,0 см, а на Рис. 4б – в случае тысячи измерений при Δ k =0,5 см.
Гистограммы на Рис. 4 иллюстрируют важное свойство большинства измерений: с ростом числа измерений их распределение стремится к некоторой определенной непрерывной кривой – предельному распределению, которая соответствует гистограмме при N ®¥ и Δ k ®0.
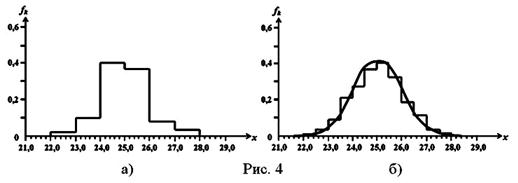
При наличии только случайных погрешностей предельное распределение представляет собой симметричную колоколообразную кривую, показанную на Рис.4б. Конечно, предельное распределение – теоретическая идеализация, которую никогда нельзя точно получить в эксперименте.
Предельное распределение определяет функцию, называемую плотностью распределения, которую обозначим f(x). Если известна функция f(x), можно разделить весь интервал значений x на малые интервалы от xk до xk +Δ xk. Тогда доля значений, попавшая в каждый такой интервал, будет Fk = f(xk)· Δ xk и формула (3.1.3), определяющая среднее значение величины, в пределе, когда все интервалы стремятся к нулю примет вид
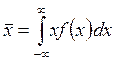 (3.1.5)
(3.1.5)
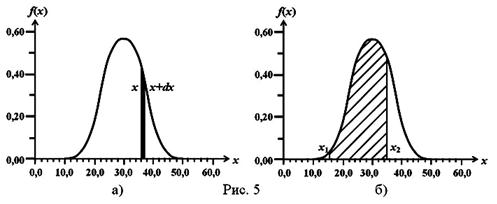
Доля измерений (при N ®¥), которая попадает в любой бесконечно малый интервал от x до x+dx, будет равна площади f(x) · dx заштрихованного участка на Рис.5а. В случае интервала конечной ширины. например от x1 до x2, доля от полного числа измерений, попадающих в данный интервал равна площади под кривой между x=x1 и x=x2 (Рис.5б). Она определяется путем интегрирования: доля измерений в интервале от x1 до x2 равна 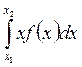 .
.
Сказанное можно выразить другим очень полезным способом:
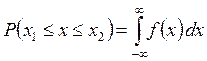 – (3.1.6)
– (3.1.6)
– данный интеграл определяет вероятность попадания любого единичного измерения в интервал от x = x1 до x = x2.
Отсюда можно сделать важное заключение: если бы было известно предельное распределение f(x) для результатов измерений данной величины x, то можно найти вероятность получения результата в любом заданном интервале x 1 £ x £ x 2.
Предельное распределение f(x) должно удовлетворять условию нормировки (аналогично (3.1.4) для дискретной функции):
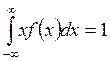 , (3.1.7)
, (3.1.7)
которое означает, что при единичном измерении вероятность получения результата в пределах от –¥ до +¥ равна единице.
Наиболее употребительной мерой, характеризующей рассеяние случайной величины, является дисперсия, обозначаемая D x и определяемая по формуле:
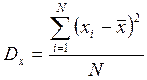 . (3.1.8)
. (3.1.8)
По аналогии с (3.1.5), когда N ®¥ дисперсия определяется через функцию распределения
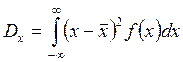 . (3.1.9)
. (3.1.9)
Квадратный корень из дисперсии называется среднеквадратичным или стандартным отклонением и обозначается sx
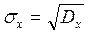 . (3.1.10)
. (3.1.10)
3.2. Функция Гаусса
В математике функция, график которой имеет форму колоколообразной кривой, называется функцией нормального распределения или функцией Гаусса. Она имеет следующий вид:
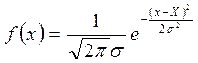 . (3.2.1)
. (3.2.1)
Функция Гаусса описывает предельное распределение результатов измерений величины x, истинное значение которой равно X. Причем при измерении величины x сказываются только случайные ошибки. Принято считать, что результаты измерений распределены нормально, если их предельное распределение описывается функцией Гаусса.
В формуле (3.2.1) величина σ является фиксированным параметром, который определяет ширину гауссовой кривой в точках перегиба. Малые значения σ приводят к распределению типа острого пика, которое соответствует более точным измерениям, в то время как большие значения σ дают широкое распределение, соответствующее измерениям с малой точностью. На Рис.6 представлены два примера графиков функций Гаусса с различными значениями величин
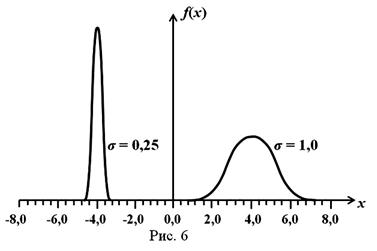
Х и σ. Видно, что величина σ в знаменателе предэкспоненциального множителя формулы (3.2.1) обеспечивает для более узкого распределения (малые σ) большую высоту в точке x = X. Это обусловлено тем, что функция Гаусса нормирована, то есть для нее выполнено условие (3.1.6). Поэтому площадь под кривой, выражающей на графике функцию Гаусса, при любых значениях σ и X должна равняться единице.
Функция Гаусса отражает следующие предположения, лежащие в основе теории случайных погрешностей и подтверждаемые опытом:
1. Погрешности результатов наблюдений принимают непрерывный ряд значений.
2. При большом числе наблюдений одинаково часто встречаются погрешности одного значения, но разных знаков.
3. Частота появления погрешностей уменьшается с возрастанием их значений.
В случае распределения Гаусса среднее значение величины X определяется, согласно (3.1.5), по формуле:
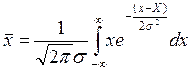 . (3.2.2)
. (3.2.2)
Интеграл вычисляется аналитически, что приводит к следующему результату:
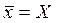 (3.2.3)
(3.2.3)
Отсюда можно сделать вывод: если результаты измерений распределены в соответствии с функцией Гаусса, то в случае бесконечно большого числа измерений среднее значение 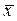 будет равно истинному значению X, которое соответствует центру функции Гаусса.
будет равно истинному значению X, которое соответствует центру функции Гаусса.
Для дисперсии (3.1.9) в случае распределения Гаусса получим
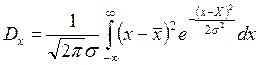 (3.2.4)
(3.2.4)
Результат аналитического интегрирования:
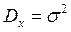 (3.2.5)
(3.2.5)
Поскольку, согласно (3.1.10), корень из дисперсии есть стандартное отклонение, то
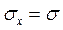 . (3.2.6)
. (3.2.6)
Следовательно: параметр σ ширины функции Гаусса есть стандартное отклонение, которое мы получили бы в случае бесконечно большего числа измерений.
3.3. Вероятность попадания результата однократного измерения в заданный интервал
Для распределения Гаусса вероятность попадания результата измерения в определённый интервал при однократном измерении, согласно (3.1.6), определяется по формуле:
P (в пределах tσ)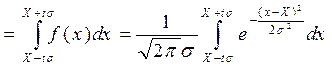 , (3.3.1)
, (3.3.1)
где t – положительное число, tσ – полуширина задаваемого интервала.
После подстановки 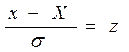 , dx = σdz получим:
, dx = σdz получим:
Р (в пределах tσ)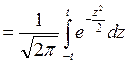 (3.3.2)
(3.3.2)
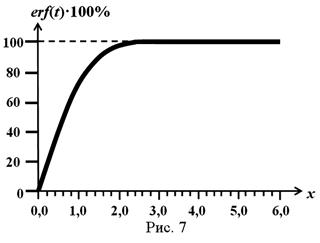 Этот интеграл называют функцией ошибок (или нормальным интегралом ошибок), который обозначается erf (t). Его значение при произвольном t аналитически не вычисляется и определяется только численными методами. В таблице 1 Приложения приведены значения функции ошибок для различных значений t. Вероятность может быть определена как в виде десятичной дроби, так и в процентах. На Рис. 7 изображена зависимость функции ошибок от параметра t в процентах.
Этот интеграл называют функцией ошибок (или нормальным интегралом ошибок), который обозначается erf (t). Его значение при произвольном t аналитически не вычисляется и определяется только численными методами. В таблице 1 Приложения приведены значения функции ошибок для различных значений t. Вероятность может быть определена как в виде десятичной дроби, так и в процентах. На Рис. 7 изображена зависимость функции ошибок от параметра t в процентах.
Из Таблицы 2 Приложения или Рис.7 видно, например, что вероятность попадания в интервал полуширина которого соответствует одному стандартному отклонению σ равна 68%, 2 σ – 95%, 3 σ – 99,7%, то есть с увеличением t вероятность попадания в интервал с пределами tσ быстро стремиться к 100%.
Используя Таблицу 2 Приложения легко определить вероятность попадания результата единичного измерения в интервал с произвольными границами x 1 и x 2, то есть когда x 1 и x 2 отличаются от X на одинаковое значение tσ.
Вероятность того, что ожидаемый результат однократного измерения окажется вне определённого интервала можно определить по формуле:
Р (вне tσ) = 100% – Р (в пределах tσ). (3.3.3)
Поэтому, например, вероятность попадания результата единичного измерения за пределы интервала с полушириной tσ от истинного значения Х очень мала и составляет всего 0,3%.
3.4. Прямые измерения
В реальных условиях число измерений конечно. Если, например, сделано N измерений величины x (то есть некоторый эксперимент независимо повторен N раз), то полученные результаты x 1, x 2, …, xN называют случайной выборкой объёма N из множества всех возможных значений величины x.
В теории обработки результатов эксперимента строго доказывается, что в этом случае наилучшей оценкой истинного значения X является выборочное среднее значение из N измерений:
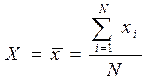 (3.4.1)
(3.4.1)
Кроме того, наилучшей оценкой стандартного отклонения σx является выборочное среднее квадратичное отклонение Sx:
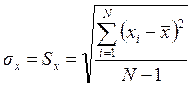 (3.4.2)
(3.4.2)
3.5. Отбрасывание результатов прямых измерений
Ранее было сказано, что среди погрешностей измерений могут встречаться промахи – погрешности, существенно превышающие ожидаемые значения при данных условиях эксперимента. Поэтому возникает естественный вопрос – какие погрешности следует считать промахами с целью исключения в дальнейшем соответствующих им результатов измерения? Эта оценка осуществляется на основе критерия Шовене.
Пусть проделано N измерений некой величины x и получены следующие результаты: x 1, x 2, …, xN. На основании этих значений по формулам (3.4.1) и (3.4.2) можно вычислить 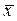 и Sx. Если имеется подозрительный результат, погрешность которого, возможно, является промахом, то для него вычисляют
и Sx. Если имеется подозрительный результат, погрешность которого, возможно, является промахом, то для него вычисляют
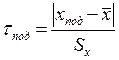 – (3.5.1)
– (3.5.1)
число выборочных стандартных отклонений, на которое xпод отличается от 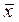 . По таблице 2 Приложения можно найти вероятность Р (вне τподSx) того, что нормальное измерение будет отличаться от
. По таблице 2 Приложения можно найти вероятность Р (вне τподSx) того, что нормальное измерение будет отличаться от 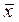 на τпод или более выборочных стандартных отклонений. Наконец, следует умножить полученную вероятность Р (вне τподSx) на полное число измерений N, чтобы получить
на τпод или более выборочных стандартных отклонений. Наконец, следует умножить полученную вероятность Р (вне τподSx) на полное число измерений N, чтобы получить
n (хуже, чем xпод) = N · P (вне τподSx), (3.5.2)
которое определяет число ожидаемых измерений, которые дают столь же плохие результаты, что и xпод. Если n <0,5, то xпод отбрасывается. В этом состоит критерий Шовене. После отбрасывания результата, не удовлетворяющего критерию Шовене, надо пересчитать 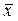 и Sx по оставшимся данным. При n >0,5 следует всё оставить без измерения.
и Sx по оставшимся данным. При n >0,5 следует всё оставить без измерения.
Рассмотрим пример: пусть произведено шесть измерений некоторой величины и получены следующие результаты: 3,8; 3,5; 3,9; 3,9; 3,4; 1,8. Среди этих результатов подозрительным является 1,8. Поэтому с учётом шести измерений рассчитываем 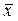 =3,4 и Sx =0,8. Значение 1,8 отличается от
=3,4 и Sx =0,8. Значение 1,8 отличается от 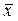 на 2 Sx. Согласно Таблицы 2 Приложения:
на 2 Sx. Согласно Таблицы 2 Приложения:
Р (вне 2 Sx) = 1 – Р (в пределах 2 Sx) = 0,05.
То есть из двадцати возможных результатов измерений приблизительно только один должен также сильно отличаться от 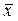 как число 1,8. В случае проведённых шести измерений ожидаемое число таких результатов n =0,05·6=0,3. Поскольку n <0,5, то, согласно критерию Шовене, подозрительный результат x=1,8 должен быть исключён, а для оставшихся значений
как число 1,8. В случае проведённых шести измерений ожидаемое число таких результатов n =0,05·6=0,3. Поскольку n <0,5, то, согласно критерию Шовене, подозрительный результат x=1,8 должен быть исключён, а для оставшихся значений 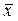 =3,7; Sx =0,23.
=3,7; Sx =0,23.
3.6. Косвенные измерения
Теперь следует привести результаты, которые получены в теории измерений для случая, когда производятся косвенные измерения величины q (x, y, …., z). Причём величины x, y, …, z могут быть зависимыми.
Пусть производится конечное число измерений, но на результат измерений оказывает влияние только случайные погрешности. Если погрешности при измерении x, y,…, z малы, то существует строгое доказательство, что наилучшей оценкой значения q является
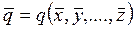 , (3.6.1)
, (3.6.1)
где 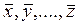 определяются по формуле (3.4.1).
определяются по формуле (3.4.1).
Оценка стандартного отклонения при косвенных измерениях определяются выражением:
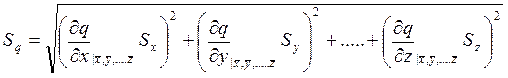 , (3.6.2)
, (3.6.2)
где Sx, Sy, …, Sz являются выборочными стандартными отклонениями, определяемыми по формуле (3.4.2). После вычисления частных производных в полученных выражениях осуществляется подстановка 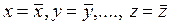 .
.
3.7. Стандартное отклонение среднего
Предположим, что результаты измерений величины x распределены нормально около истинного значения X с шириной σx. Необходимо узнать, какова надёжность среднего значения для N измерений. Для ответа на этот вопрос представим себе, что N измерений повторяются много раз, причём в каждом случае определяется среднее значение 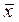 . Нас интересует, как распределены полученные значения
. Нас интересует, как распределены полученные значения 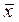 .
.
Величина 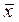 есть простая функция измеренных значений x 1, x 2, …, xN
есть простая функция измеренных значений x 1, x 2, …, xN
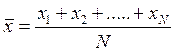 . (3.7.1)
. (3.7.1)
Поэтому можно найти распределение 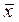 с помощью расчёта ошибок для косвенных измерений.
с помощью расчёта ошибок для косвенных измерений.
Поскольку каждое из измеренных значений x 1, x 2, …, xN распределено нормально, то очевидно, что и 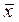 также имеют нормальное распределение. Так как истинным значением для x 1, x 2, …, xN является X, то и истинным значением
также имеют нормальное распределение. Так как истинным значением для x 1, x 2, …, xN является X, то и истинным значением 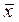 является также X. Следовательно, полученные значения
является также X. Следовательно, полученные значения 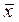 распределены нормально около истинного значения X. Ширину этого распределения можно найти по формуле:
распределены нормально около истинного значения X. Ширину этого распределения можно найти по формуле:
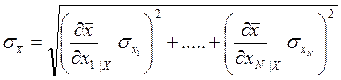 . (3.7.2)
. (3.7.2)
Но:
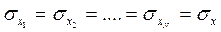 , (3.7.3)
, (3.7.3)
а из (3.7.1) следует:
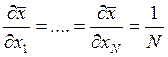 . (3.7.4)
. (3.7.4)
Следовательно, вместо (3.7.2) получаем:
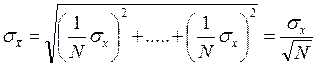 . (3.7.5)
. (3.7.5)
Эту величину называют стандартным отклонением среднего. Видно, что при N®¥ значение 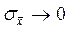 .
.
Вывод: значения 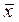 распределены нормально с центром, равным истинному значению и с шириной
распределены нормально с центром, равным истинному значению и с шириной 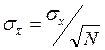 ; другими словами, если найдено однажды
; другими словами, если найдено однажды 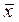 , то вероятность попадания этого значения в интервал
, то вероятность попадания этого значения в интервал 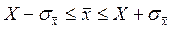 равна 68%.
равна 68%.
Для оценки стандартного отклонения среднего, которое обозначим 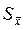 , используют формулу
, используют формулу
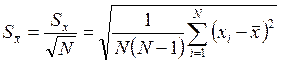 (3.7.6)
(3.7.6)
Величину 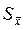 называют выборочным стандартным отклонением среднего. Видно, что при увеличении числа измерений N растёт точность измерения. Стандартное отклонение среднего при косвенных измерениях может быть определено по формуле:
называют выборочным стандартным отклонением среднего. Видно, что при увеличении числа измерений N растёт точность измерения. Стандартное отклонение среднего при косвенных измерениях может быть определено по формуле:
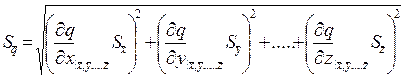 (3.7.7)
(3.7.7)
Рассмотрим следующий пример: определим выражение для стандартного отклонения величины q, которая связана с величинами x, y, z, определяемыми прямыми измерениями, следующим соотношением:
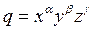 , (3.7.8)
, (3.7.8)
где α, β, γ – точные числа.
Для частных производных получаем:
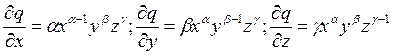 . (3.7.9)
. (3.7.9)
После подстановки (3.7.9) в (3.7.7) имеем:
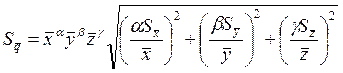 . (3.7.10)
. (3.7.10)
3.8. Распределение Стьюдента
Ранее было показано, что величина 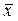 является лишь наилучшей оценкой истинного значения измеряемой величины. Вместе с этим, наилучшей оценкой стандартного отклонения среднего является величина
является лишь наилучшей оценкой истинного значения измеряемой величины. Вместе с этим, наилучшей оценкой стандартного отклонения среднего является величина 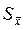 . Таким образом, мы имеем дело с некоторыми приближениями. Ясно, что распределение случайных погрешностей будет тем существенней отличаться от функции Гаусса, чем меньше выполнено измерений.
. Таким образом, мы имеем дело с некоторыми приближениями. Ясно, что распределение случайных погрешностей будет тем существенней отличаться от функции Гаусса, чем меньше выполнено измерений.
Английский химик и математик В.С. Госсет, публиковавший свои работы под псевдонимом Стьюдент, получил формулу для нахождения распределения погрешностей средних значений, получаемых при конечном числе измерений. Причём им была получена зависимость вероятности попадания получаемого результата в определённый интервал от числа измерений. Однако эта зависимость имеет сложный характер и не выражается через элементарные функции.
На основе распределения Стьюдента были составлены таблицы коэффициентов Стьюдента tα , n, которые показывают во сколько раз нужно увеличить величину 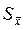 , чтобы при определённом числе измерений n получить задаваемую вероятность (надёжность) n. Коэффициенты Стьюдента представлены в Таблице 1 Приложения.
, чтобы при определённом числе измерений n получить задаваемую вероятность (надёжность) n. Коэффициенты Стьюдента представлены в Таблице 1 Приложения.
В результате можно записать:
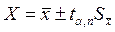 , (3.8.1)
, (3.8.1)
где 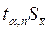 – доверительный интервал, который означает, что истинное значение измеряемой величины находится в интервале
– доверительный интервал, который означает, что истинное значение измеряемой величины находится в интервале 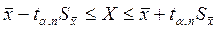 с вероятностью или надёжностью α, где
с вероятностью или надёжностью α, где
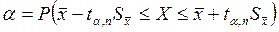 . (3.8.2)
. (3.8.2)
§4. Средства измерений
Под средствами измерений понимается всё многообразие измерительных инструментов и приборов. Средства измерений разнообразны, но имеют общее назначение и поэтому имеют общую теорию погрешностей. Основной задачей этой теории является расчёт результирующей погрешности средств измерений по отдельным составляющим погрешностей.
4.1. Погрешности средств измерений
Погрешности средства измерений может иметь и систематическую, и случайную составляющие. Систематические составляющие вызываются: неточным нанесением отметок на циферблат; изменением со временем упругих свойств пружины, создающей противодействующий момент; неточной подгонкой сопротивлений резисторов и другими причинами технологического характера. Случайная составляющая погрешности вызывается, например, трением в опорах подвижной части прибора; нестабильностью переходного сопротивления электрических контактов переключателей и другими причинами случайного характера.
Погрешность средств измерений, то есть инструментальная или приборная ошибка, определяется суммой систематической и случайной ошибок.
Ошибки измерительных приборов зависят от условий их работы, температуры, влажности, давления, уровня вибраций и т.д. Условия, при которых делается градуировка приборов, определяются соответствующими стандартами и называются нормальными условиями. Ошибка приборов при нормальных условиях называется основной. Условия, при которых делаются измерения часто не совпадают с нормальными. Возникающая вследствие этого ошибка называется дополнительной.
Градуировку средств измерения осуществляют с помощью образцовых приборов, суммарная погрешность которых, согласно требованиям законодательной метрологии, не должна быть более 1/3 погрешности градуируемых средств измерения. При градуировке получают на графике точки, расположенные в некоторой полосе, по которой проводят плавную среднюю кривую, которую принимают за номинальную градуировочную характеристику средства измерения.
Воздействие различных причин при получении градуировочной характеристики прибора приводит к тому, что многократно снятые характеристики прибора или серии однотипных приборов занимают на графике некоторую полосу, которую называют полосой погрешностей данного типа или данного экземпляра прибора. Полоса погрешностей является обобщённой характеристикой результирующей инструментальной погрешности прибора. Параметры полосы погрешностей определяются положением её границ. На основе полосы погрешностей для каждого типа приборов устанавливаются нормируемые значения погрешности. Под нормируемыми значениями погрешности понимаются границы предельно допустимых значений модуля реальных погрешностей.
Для учёта систематической ошибки прибора используется её рандомизация, сущность которой в следующем. Систематическая ошибка прибора изменяется от одного прибора к другому. Для простоты вся совокупность приборов данного вида характеризуется функцией плотности, стандартным отклонением или интервалом, в который с определённой вероятностью попадает систематическая ошибка 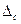 , поэтому при работе с прибором в силу отсутствия информации об ошибке конкретного прибора используют распределение ошибок для всей совокупности приборов, то есть учитывают систематическую ошибку как случайную.
, поэтому при работе с прибором в силу отсутствия информации об ошибке конкретного прибора используют распределение ошибок для всей совокупности приборов, то есть учитывают систематическую ошибку как случайную.
Правила, согласно которым назначаются предельные границы погрешностей и форма их записи, то есть вся процедура нормирования погрешностей средств измерения, основывается на системе стандартов, обеспечивающих единство измерений, при этом для разных средств измерения используется абсолютные, относительныеилиприведённые значения погрешностей.
Абсолютная погрешность выражается в единицах измеряемой величины, например, в милливольтах, амперах, кельвинах и т.д. её использование удобно для однозначных мер, но мало удобно для широкодиапазонных приборов. Пределы допускаемой абсолютной погрешности устанавливаются по формулам:
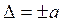 (4.1.1)
(4.1.1)
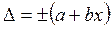 , (4.1.2)
, (4.1.2)
где ∆ – пределы допускаемой абсолютной погрешности, выраженные в единицах измеряемой величины; x – значение измеряемой величины; a, b – положительные числа, не зависящие от x.
Приведённая погрешность определяется как отношение абсолютной погрешности прибора, выраженной в единицах измеряемой величины, и протяжённости диапазона измерения прибора и выражается в десятичных дробях или в процентах. Пределы допускаемой приведённой основной погрешности устанавливаются по формуле:
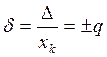 , (4.1.3)
, (4.1.3)
где δ – пределы допускаемой основной приведённой погрешности в процентах; ∆ – устанавливается по формуле (4.1.1), что означает – ширина полосы погрешностей остаётся постоянной на всём диапазоне измерений, то есть остаются постоянными пределы допускаемой абсолютной основной погрешности; xk – нормирующее значение, выраженной в тех же единицах, что и ∆ (как правило, ∆ – предел измерения на данном диапазоне, но если нуль шкалы находится посередине, под ∆ – понимают модуль разности положительного и отрицательного пределов); q – отвлечённое положительное число, выбираемое из следующего ряда:
1·10 n, 1,5·10 n, 2·10 n, 2,5·10 n, 4·10 n, 5·10 n, 6·10 n, (4.1.4)
где n = 1, 0, – 1, – 2 и так далее.
Число q определяет класс точности прибора. Так, согласно ГОСТ 1845-59, электроизмерительные приборы делятся на восемь классов точности: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4. Класс точности определяет наибольшую приведённую ошибку для всего рабочего диапазона в процентах. Из формулы (4.1.3) следует, что наибольшая абсолютная погрешность для всего диапазона:
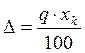 (4.1.5)
(4.1.5)
Например, для милливольтметра со шкалой до 50 мВ, имеющего класс точности 0,5 абсолютная погрешность не превышает ∆=±0,5·50 мВ /100=±0,5 мВ. Полная погрешность измерения должна включать также погрешность отсчёта по шкале.
Пределы допускаемой относительной основной погрешности средств измерения устанавливаются по формуле:
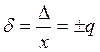 , (4.1.6)
, (4.1.6)
где q – отвлечённое положительное число, выбираемое из ряда (4.1.4); x – показания прибора. Так как класс точности прибора q – величина постоянная, абсолютная приборная погрешность
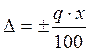 (4.1.7)
(4.1.7)
оказывается пропорциональной x, то есть возрастает от нуля, в начале диапазона измерений, до максимального значения в конце. Примером таких приборов могут служить магазин ёмкостей (ГОСТ 6746-75, класс точности 0,5) или магазин сопротивлений (ГОСТ 7003-64, класс точности 0,2). На самом деле абсолютная приборная погрешность практически никогда не может обращаться в нуль в начале диапазона измерений. Для учёта этого факта относительная погрешность прибора может устанавливаться по формуле:
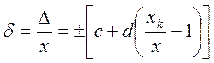 , (4.1.8)
, (4.1.8)
где xk – больший по модулю из пределов измерений; c и d – положительные числа, выбираемые из ряда (4.1.4). Класс точности прибора в этом случае обозначается двумя числами, разделёнными косой чертой c / d. Примером такого прибора может служить магазин сопротивлений (ГОСТ 23734-79) класса точности 0,2/6·10-6.
4.2. Погрешности некоторых измерительных приборов
ИЗМЕРИТЕЛЬНЫЕ ЛИНЕЙКИ
а) Стальные измерительные линейки (ГОСТ 427-56)
Деления нанесены через 1 мм. Допускаемая предельная погрешность при длине линейки 300 мм, 500 мм и 1000 мм составляет, соответственно, ±0,10 мм; ±0,15 мм; ±0,20 мм. Ошибку округления в определении долей деления шкалы на глаз следует учесть в соответствии с п. 4.3. Но и при соблюдении описанных в этом параграфе правил, ошибку отсчёта долей деления на глаз следует принимать не менее чем 0,2 деления.
б) Деревянные и пластмассовые линейки (ГОСТом не нормируются).
За основную предельную ошибку для деревянных линеек следует принимать ±0,5 мм, а для пластмассовых ±1,0 мм.
ШТАНГЕНЦИРКУЛИ (ГОСТ 166-73)
Выпускаются различные штангенциркули, пределы измерения которых изменяются от 125 мм до 2500 мм. Основной частью штангенциркуля является нониус – отчетная устройство с дополнительной шкалой, цена деления которой меньше, чем цена деления основной шкалы. Точность штангенциркуля с нониусов равна разности цены деления основной шкалы и цены деления шкалы нониуса. Для штангенциркулей с точностью 0,1 мм предельная основная приборная погрешность прибора равна ±0,1 мм, а для штангенциркулей с точностью 0,05 мм составляет ±0,05 мм. Кроме этого следует учитывать ошибку округления. Её максимальное значение равно половине точности.
МИКРОМЕТРЫ (ГОСТ 6507)
Микрометры позволяют производить изменения точнее, чем штангенциркули. Цена деления круговой шкалы микрометра равна 0,01 мм. Основная предельная приборная ошибка для микрометра при измерении размеров до 3 мм не превышает ±0,002 мм, а при измерении больших размеров не превышает ±0,004 мм. При работе в физической лаборатории следует также учитывать погрешность округления при измерении и погрешность при установке нулевого деления. Максимальная погрешность округления, очевидно, равна ±0,005 мм.
ИЗМЕРЕНИЕ ВРЕМЕНИ
В лабораториях при измерении времени часто используются механические секундомеры с ценой деления 0,1 с или 0,2 с. Основная предельная ошибка этих секундомеров равна цене деления. Вместе с этим механические секундомеры обладают ошибкой хода, которая, например, для секундомеров типа С-1, С-2, СМ-60 могут достигают ±1,5 с за 30 минут хода (ГОСТ 5073-62). Следует также учитывать, что при включении и остановке механических секундомеров возникает субъективная ошибка, связанная с несовершенством органов чувств (в данном случае с неидеальной реакцией) любого экспериментатора. Эта погрешность, как показали специальные исследования, может достигать ±0,3 с. В учебных лабораториях также используются электронные счётчики-секундомеры ССЭШ, точность которых составляет 0,01 с. Основная предельная погрешность для этих приборов (ГОСТ 6836-72) составляет ±(0,02· t +0,01) с.
НАБОР ГИРЬ
По допускаемой погрешности гири делятся на пять классов точности. Набор гирь, используемых в учебной лаборатории, соответствует четвертому классу точности. В. представленной таблице указываются основные предельные погрешности этих гирь.
Таблица 2
| Номинальное значение, г | |||||||
| Основная предельная погрешность, мг | ±40 | ±30 | ±20 | ±12 | ±8 | ±6 | ±4 |
| Номинальное значение, мг | |||||||
| Основная предельная погрешность, мг | ±3 | ±2 | ±1 | ±1 | ±1 | ±1 | ±1 |
Набор гирь для настольных (торговых) весов ВТ-200 относится к пятому классу. Допускаемые отклонения гирь, используемых с этими весами, указаны в следующей таблице.
Таблица 3
| Номинальное значение, г | ||||||||
| Основная предельная погрешность, мг | ±600 | ±400 | ±300 | ±200 | ±150 | ±100 | ±60 | ±40 |
4.3. Ошибки округления
При считывании показаний со шкалы прибора всегда возникает ошибка, связанная с округлением числа, которую рассматривают как случайную величину. Функция распределения этой случайной величины может быть определена следующей формулой.
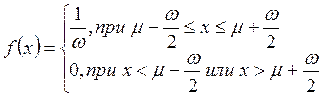 (4.3.1)
(4.3.1)
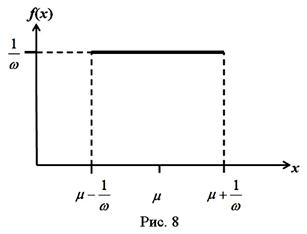 Здесь ω – цена деления прибора или та ее доля до которой возможен отсчет; μ – значение физической величины, соответствующее определенной отметке шкалы. Такое распределение называют прямоугольным или равномерным. График этой функции представлен на Рис. 8.
Здесь ω – цена деления прибора или та ее доля до которой возможен отсчет; μ – значение физической величины, соответствующее определенной отметке шкалы. Такое распределение называют прямоугольным или равномерным. График этой функции представлен на Рис. 8.
Зная функцию распределения f(х) можно определить среднее значение 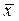 (см. формулу (3.1.5)):
(см. формулу (3.1.5)):
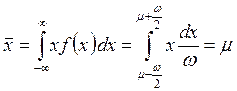 (4.3.2)
(4.3.2)
Вероятность того, что случайная величина лежит в интервале 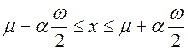 (0 ≤ α ≤ 1) равна площади прямоугольника со сторонами
(0 ≤ α ≤ 1) равна площади прямоугольника со сторонами 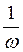 и αω:
и αω:
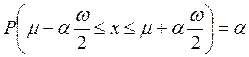 (4.3.3)
(4.3.3)
Таким образом, задавая определенную вероятность α, мы можем определить интервал, в который случайная величина х будет заключена с этой вероятностью.
4.4. Неравенство Чебышева
В ряде случаев функция распределения может быть неизвестной, однако при этом возникает вопрос о вероятности попадания случайной величины в заданный интервал. Оказывается, ответ на этот вопрос, можно получить, если известно среднее значение и дисперсия случайной величины. Для этого случая П.Л.Чебышев получил неравенство для оценки вероятности того, что случайная величина х не отличается от своего среднего значения 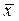 на величину, большую γσx (γ – положительное число):
на величину, большую γσx (γ – положительное число):
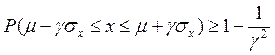 . (4.4.1)
. (4.4.1)
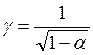
Для определения вероятности P = α отсюда можно найти число γ >0, при котором неравенство (4.4.1) будет выполняться:
 . (4.4.2)
. (4.4.2)
Другими словами, неравенство Чебышева утверждает, что вероятность попадания случайной величины х в интервал 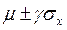 , не меньше α (γ – определяется из (4.4.2)).
, не меньше α (γ – определяется из (4.4.2)).
§5. Правила математической обработки результатов эксперимента
15.1. Прямые измерения
1. Результаты измерений записать в таблицу.
2. Вычислить выборочное среднее из N измерений:
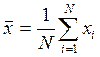 (5.1.1)
(5.1.1)
3. Если какой-либо результат измерения резко отличается по своему значению от остальных, то следует проверить не обусловлен ли он промахом по процедуре, изложенной в §3.5. Если это так, то данный результат нужно отбросить и повторить расчет по формуле (5.1.1).
4. Вычислить выборочноё стандартное отклонение среднего:
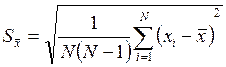 (5.1.2)
(5.1.2)
5. Определить различные составляющие погрешностей средств измерений для вероятности 68%. Срединих:
Δп – ошибка прибора; если ошибка прибора задается как предельная (максимальная) Δпр, то для α =68%
Δп 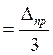 ; (5.1.3.)
; (5.1.3.)
Δокр – ошибка округления
Δокр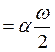 , (5.1.4.)
, (5.1.4.)
где ω – цена деления прибора, или та ее доля, до которой возможен отсчет;
Δсуб – субъективная ошибка.
6. Вычислить доверительная интервал для α=68% по формуле:
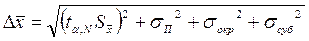 (5.1.5)
(5.1.5)
7. Результат записать в виде:
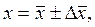 вероятность a =(число). (5.1.6)
вероятность a =(число). (5.1.6)
8. Если для величины х известно значение систематической ошибки А (она может быть положительной или отрицательной), то извыборочного среднего нужно вычесть величину этой ошибки, то есть найти разность
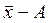 , (5.1.7)
, (5.1.7)
на которую следует заменить величину 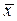 . Напомним, что задавая различное значение вероятности a можно определить соответствующее
. Напомним, что задавая различное значение вероятности a можно определить соответствующее 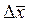 .
.
15.2. Косвенные измерения
Пусть требуется измерить величину q = q (x 1, x 2, …, xn), где x 1, x 2, …, xn определяют прямыми измерениями.
1. Для каждой величины xi произвести расчеты по процедуре, описанной в п. 5.1 и записать результаты в виде:
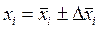 , вероятность a =(число). (5.2.1)
, вероятность a =(число). (5.2.1)
2. Вычислить среднее значение функций
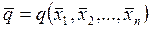 . (5.2.2)
. (5.2.2)
3. Вычислить доверительный интервал для величины 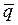 , соответствующий вероятности a =68% по формуле:
, соответствующий вероятности a =68% по формуле:
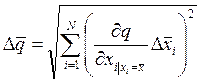 (5.2.3)
(5.2.3)
Если, например, величина 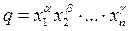 (α, β, …, γ – точные числа), то доверительный интервал, как следует из (5.2.3), удобно вычислять по формуле:
(α, β, …, γ – точные числа), то доверительный интервал, как следует из (5.2.3), удобно вычислять по формуле:
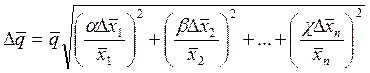 (5.2.4)
(5.2.4)
4. Окончательный результат записать в виде:
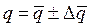 , вероятность a =(число) (5.2.5).
, вероятность a =(число) (5.2.5).
5. При необходимости доверительный интервал можно рассчитать для большей вероятности, используя формулу (4.4.2).
§6. Метод наименьших квадратов
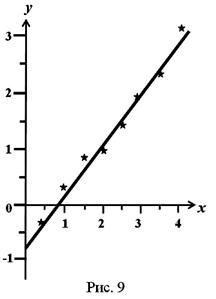
При выполнении эксперимента часто измеряют две величины х и у, причем у является функцией х. Найденные значения откладывают на графике и пытаются построить кривую, которая наилучшим образом отражает зависимость y = f (x). Ограничимся случаем линейной зависимости
у = b x + a (6.1)
Задача состоит в том, чтобы найти параметры b и α, при которых прямая, выражающая на графике зависимость (16.1), наилучшим образом проходила бы через экспериментальные точки.
 Пусть величины х и у измеряются прямым способом, их случайные погрешности распределены по нормальному закону, а систематическими погрешностями можно пренебречь.
Пусть величины х и у измеряются прямым способом, их случайные погрешности распределены по нормальному закону, а систематическими погрешностями можно пренебречь.
Представим все экспериментальные данные хi и yi на графике. Геометрически задача измерения a и b состоит в определении параметров некоторой прямой: значения ординаты при нулевом значении абсциссы и тангенса угла наклона соответственно.
По имеющимся точкам на графике можно провести не единственную прямую. Однако, в теория доказывается, что наилучшей прямой будет такая, для которой сумма квадратов разностей

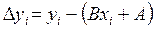 (6.2)
(6.2)
будет минимальна, то есть
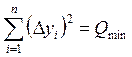 . (6.3)
. (6.3)
Это условие выполняется, если производные будут равны нулю:
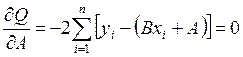 , (6.4)
, (6.4)
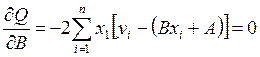 . (6.5)
. (6.5)
Отсюда находим:
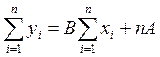 , (6.6)
, (6.6)
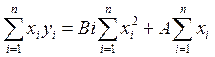 . (6.7)
. (6.7)
Из (6.6) и (6.7) следует, что наилучшей оценкой В является следующее выражение:
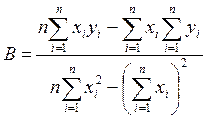 , (6.8)
, (6.8)
а оценкой А:
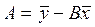 , (6.9)
, (6.9)
где 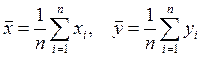 . (6.10)
. (6.10)
Используя (6.10) формулу (6.8) можно преобразовать к виду:
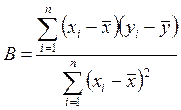 (6.11)
(6.11)
Для определения погрешностей бывает достаточно вычислить стандартное отклонение коэффициента В или интервал, в котором с установленной вероятностью может находиться коэффициент b. Стандартное отклонение коэффициента В определяется по формуле:
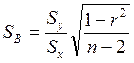 , (6.12)
, (6.12)
в которой
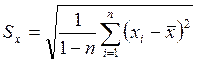 , (6.13)
, (6.13)
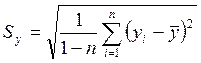 , (6.14)
, (6.14)
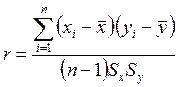 , (6.15)
, (6.15)
Интервал, в котором с задаваемой вероятностью a может находиться коэффициент В, записывается в виде: