Вращающиеся и работающие на кручение стержни называ­ют валами

Рис. 13.1. Рис. 13.2.

Рис. 12.3.

Рис. 12.2.

Рис. 12.1.

Рис. 11.5.

Рис. 11.3. Рис. 11.4.

Рис. 11.2.

Рис. 11.1.

Рис. 10.3.

Напряжение, при котором происходит рост деформаций без увеличения нагрузки, называется пределом текучести и обозна­чается sт.

Для стали СтЗ предел текучести равен 230 МПа.

Ряд материалов при растяжении дает диаграмму без выра­женной площадки текучести; для них устанавливается так назы­ваемый условный предел текучести.

Напряжение, при котором остаточная деформация равна 0,2%, называется условным пределом текучести. Условный предел текучести обозначается s_0,2. К материа­лам, для которых определяется условный предел текучести, относятся дюралюминий, бронза, высокоуглеродистые и легиро­ванные стали.

Удлинившись на некоторую величину при постоянном значе­нии силы, т. е. претерпев состояние текучести, материал снова приобретает способность сопротивляться растяжению (упрочня­ется) и диаграмма за точкой D поднимается вверх.

Точка Е диаграммы соответствует наибольшему условному напряжению, называемому пределом прочности или временным сопротивлением. Для стали СтЗ предел прочности составляет s_вр = 380 МПа.

При достижении напряжением величины предела прочности на образце появляется резкое местное сужение, так называемая шейка (рис. 10.3). Площадь сечения образца в шейке быстро уменьшается и, как следствие, падает усилие и условное напря­жение. Разрыв образца происходит по наименьшему сечению шейки.

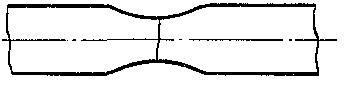
Кроме перечисленных выше характеристик прочности мате­риала при испытании на растяжение определяют также относи­тельное остаточное удлинение при разрыве e, являющееся важ­ной характеристикой пластичности материала:

;

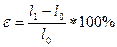где l₀ – первоначальная расчетная длина образца [см. рис. 10.1]; l₁ – расчетная длина образца после разрыва. Она изме­ряется после стыковки двух частей разорванного образца. Определенное таким путем удлинение является некоторым средним удлинением, так как деформации распределяются по длине образца неравномерно. Наибольшее удлинение возникает в месте разрыва. Оно называется истинным удлинением при разрыве.

Второй характеристикой пластичности материала является относительное остаточное сужение при разрыве

;

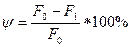где F₁ – первоначальная площадь поперечного сечения; F₀ – площадь поперечного сечения в наиболее тонком месте шейки после разрыва.

Величина y характеризует свойства пластичности более точно, чем е_л, поскольку она в меньшей степени зависит от фор­мы образца.

Тема №11. НАПРЯЖЕНИЯ ПО НАКЛОННЫМ СЕЧЕНИЯМ ПРИ ОСЕВОМ РАСТЯЖЕНИИ ИЛИ СЖАТИИ

Правильно оценить опас­ность, угрожающую прочности стержня, можно, лишь зная полно­стью его напряженное состояние, а это требует уменья вы­числять напряжения не только по сечению, перпенди­кулярному к оси, а по любому.

Вычислим напряжения, действующие по какому-либо наклонному сече­нию. Возь­мем призматический стержень, растянутый силами Р (рис. 11.1). Раз­делим его на две части: I и II сечением тп, составляющим угол a с попереч­ным сечением mk, перпен­дикулярным к оси. Тот же угол составляют между собой и нормали к этим сечениям.

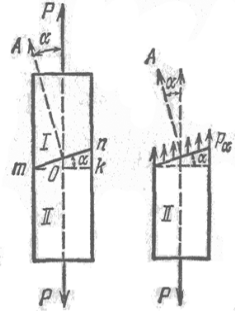
За положительное направление отсчета этого угла возьмем направ­ление против часовой стрелки. Нормаль ОА, направлен­ную на­ружу по отношению к отсеченной части стержня, будем называть внешней нормалью к сечению тп. Площадь сечения mk обозначим F_o, пло­щадь же сечения тп обозначим F_a.

Для нахождения напряжений, передающихся через намеченное сечение от верхней (I) части на нижнюю (II), отбросим мысленно верхнюю часть и заменим действие ее на нижнюю напряжениями р_a.

Для равновесия нижней части напряжения р_a должны уравнове­шивать силу Р и быть направлены параллельно оси стержня. В дан­ном случае на­пряжения уже не перпендикулярны к той площадке, по которой они дейст­вуют. Величина их тоже будет иной, чем для площадки mk.

Сделав предположение, что в достаточном удалении от мест при­ложения внешних сил Р напряжения р_a равномерно распределены по площади на­клонного сечения тп, найдем

.

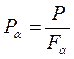Но так как F_a=F/cos a, то

.

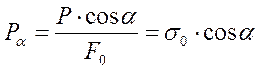где s₀=P/F_o – нормальное напряжение по площадке mk, перпендикуляр­ной к растягивающей силе.

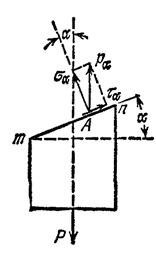
При изменении угла a меняется и величинапол­ных напряжений р_а, дейст­вующих по проведенной площадке. Чтобы при лю­бом угле наклона а иметь дело всегда с одними и теми же видами напряже­ний, разложим напряжения р_а на две составляющие: в плоскости тп и перпенди­кулярно к ней (рис. 11.2). Та­ким образом, напряжение р_а, действующее в точке А площадки тп, мы заменяем двумя взаимно перпенди­кулярными напряжениями: нормальным напряже­ниемs_а и касательным напряжением t_a.

Величины этих двух напряжений будут меняться в зависимости от изме­нения угла а между нормалью к площадке и нап­равлением растягивающей силы. Из рис. 11.2 имеем

s_a = p_a× cos a = s₀ × cos²a, (1).

t_a = p_a×sin a = s₀ × sin a × cos a = 0,5s₀ × sin2a. (2).

Установим следующие условия относительно знаковнапряжений s_a и t_a. Растягивающиенапряжения s_a, т. е. совпадающие с на­правлением внешней нормали, будем считать положительными;нор­мальные напряжения обрат­ногонаправления – сжимающие– будем принимать со знаком минус.

Касательноенапряжение будем считать положительным, если при пово­роте вектора t против часовой стрелки на 90° его направле­ние совпадет с на­правлением внешней нормали. Обратное направ­ление t будем считать отри­цательным.

На рис. 11. 3 показаны принятые условия относительно знаков a и t.

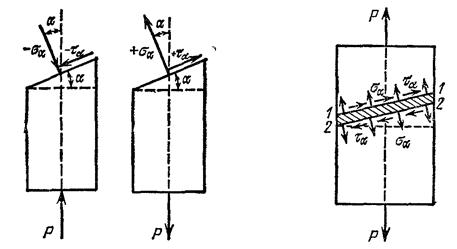
При любом угле наклона площадки a мы всегда будем иметь дело лишь с двумявидами напряжений, действующих в каждой точке проведенного разреза: с нормальным и касательным напряже­ниями.

На рис. 11.4 показано действие этих напряжений на тонкий слой материала (на рисунке заштрихованный), выделенный из растяну­того стержня двумя параллельными сечениями 1 – 1 и 2 – 2. К каж­дой из плоскостей приложены и нормальные растягивающие напря­жжения s_a,и касательные t_a, вызываю­щие сдвиг сечений 1 – 1 и 2 – 2, параллельно одно другому.

Таким образом, наличие двух видов напряжений приводит к двум видам деформации: удлинению (или укорочению) и деформации сдвига. Этому со­ответствуют и два вида разрушения материала – путем отрыва и путем сдвига, что наблюдается и в опытах на рас­тяжение.

Для проверки прочности материала стержня необходимо найти наи­большиезначения напряжений s_a и t_a, величины которых зави­сят от поло­жения площадки тп.

Из формул (1) и (2) следует, что s_a достигает своего наиболь­шего значе­ния, когда cos²a будет равен единице и угол a=0. Мак­симум же t_a получится при sin2a=l, т. е. при 2a=90° и a=45°. Величины этих наибольших напряже­ний будут равны

mах s_a = s₀ = 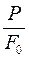; max t_a = 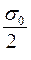. (3)

Таким образом, наибольшие нормальные напряжения возникают в данном случае по площадкам, перпендикулярным к оси стержня; наи­большие касательные напряжения действуют по площадкам, состав­ляющим угол 45° с направлением оси стержня, и равны поло­вине наи­больших нормальных напряжений.

Понятие о главных напряжениях. Виды напряжен­ного состояния материала.

На практике, возможны случаи, когда под дей­ствием внешних сил эле­мент материала подвергается растяжению или сжатию по двум и трем на­правлениям, т. е. находится в усло­виях сложного напряженного состояния.

При простом растяжении возможны напряжения двух видов – нормаль­ные и касательные. Из формул (1) и (2) следует, что по сечениям, пер­пен­дикулярным к оси растянутого стержня (a =0), возникают только нормальные напря­жения (t =0), а по сечениям, параллельным его оси (a =90°), нет ни нор­мальных, ни ка­сательных напряжений (s=0 и t =0).

Такие площадки, по которым нет касатель­ных напряжений, называются главными; нор­мальные напряжения, действующие по этим площадкам, назы­ваются главными напряже­ниями.

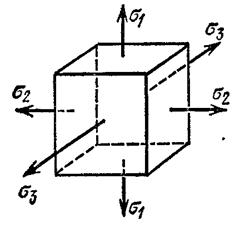
В каждой точке любого напряженного тела можно провести три взаимно пер­пендикулярные главные площадки, через которые передаются три главных (нормаль­ных) напряжения; из них два имеют экстре­мальные значения; одно яв­ляется наибольшим нор­мальным напряжением, дру­гое – наи­меньшим, третье – промежуточное. В каждой точке напряженного тела можно выделить элементар­ный кубик; гранями кото­рого служат главные пло­щадки. Материал кубика растягивается или сжимается тремя взаимно перпендику­лярными главными напря­жениями, пере­дающимися через эти грани (рис. 11.5).

В случае простого растяжения одна главная площадка в каждой точке перпендикулярна к оси стержня (a=0°), а две дру­гие параллельны этой оси (a=90°). Так как по первой главной пло­щадке нормальное напряжение не равно нулю (s_a≠0), а по двум другим оно обращается в нуль, то при простом растяжении и сжатии в каждой точке стержня из трех главных напряжений только одно не равно нулю; оно направлено параллельно растягивающей силе и оси стержня. Такое напряженное состояние материала называется ли­нейным (или одноосным). Выделенный из стержня элемент растя­гивается лишь в одном направлении.

На практике встречаются случаи, когда элемент материала, в виде ку­бика, подвергается растяжению или сжатию по двум вза­имно перпендику­лярным направлениям или по всем трем (рис. 5). Случай работы материала, когда два главных напряжения не равны нулю, называется плоским (или двухосным) напряженным состояни­ем. Если же все три главных напряжения не равны нулю в рассмат­риваемой точке, то налицо самый общий случай распределения на­пряжений в мате­риале – объемное (трехосное) напряженное состоя­ние; элементарный кубик будет подвергаться растяжению или сжа­тию по всем трем взаимно перпен­дикулярным направлениям.

Главные напряжения условимся в дальнейшем обозначать бук­вами s₁, s₂, s₃. Нумерацию главных напряжений установим таким образом, чтобы s₁ обозначало наибольшее по алгебраической величи­не, а s₃ – наименьшее на­пряжение.

Таким образом, мы различаем три вида напряженного состояния:

1) объемное напряженное состояние – когда все три главных напряже­ния не равны нулю (например, случай растяжения или сжа­тия по трем вза­имно перпендикулярным направлениям);

2) плоское напряженное состояние – когда одно главное на­пряжение равно нулю (случай растяжения или сжатия по двум направлениям);

3) линейное напряженное состояние – когда два главных на­пряжения равны нулю (случай растяжения или сжатия в одном направлении).

Тема №12. СДВИГ

Напряженное состояние и деформации при чистом сдвиге

Если на гранях элемента действуют только касательные напряжения (рис.12.1), то такой вид напряженного состояния называется чистым сдвигом. Площадки, по которым действуют только касательные напряжения, называют­ся площадками чистого сдвига.

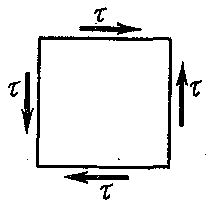
При чистом сдвиге главные напряжения получаются равными по значению и противопо­ложными по знаку: 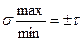, т. е. одно главное напряжение – растягивающее, другое – сжимающее (рис. 12.2).

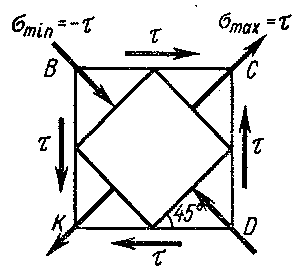
Так как отличны от нуля два главных напряжения, то сдвиг представляет собой частный случай двухосного напряженного состояния.

Главные площадки наклоне­ны под углом 45° к направлению площадок чистого сдвига (рис. 12.2).

Рассмотрим теперь деформации при сдвиге.

Элемент KBCD, прямоугольный до деформации (рис. 12.3, а), после деформации сдвига примет вид KB'C'D (грань KD считаем закрепленной).

Угол g₁ называется угловой де­формацией или углом сдвига.

Опыты показывают, что для многих материалов до известных пределов нагружения между напря­жениями и деформациями при сдви­ге имеет место линейная зависимость

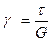; – которая выражает закон Гука при сдвиге.

Постоянную G называют модулем сдвига (модулем упругости второго рода); – он характе­ризует способность материала сопротивляться деформации сдвига.

Линейная зависимость между t и g справедлива до тех пор, пока касательные напряжения не превзойдут предела пропорци­ональности при сдвиге.

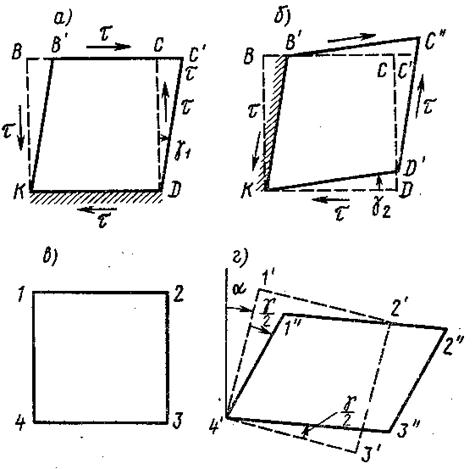
Из свойства взаимности касательных напряжений легко установить свойство взаимности угловых деформаций. Действи­тельно, если закрепить грань KD (рис. 12.3, а), то получим для угла сдвига

.

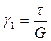Закрепив теперь грань KB' (рис. 11.3, 6), получим для угла g₂

.

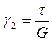Так как равны правые части, то равны и левые, т. е.

|g₁| ₌ |g₂|.

Следовательно, угловые деформации двух взаимно перпен­дикулярных площадок равны по значению и противоположны по знаку (свойство взаимности угловых деформаций).

Таким образом, картина перемещений элемента 1234 в ре­зультате линейных и угловых деформаций представлена на рис.12.3, г.

Можно представить, что сначала элемент 1234, как абсолют­но жесткий, перемещается в положение 1'2'3'4', поворачиваясь на угол a. Затем в результате линейных деформаций происходит удлинение сторон 12 и 43 и укорочение сторон 14 и 23. В резуль­тате угловых деформаций происходит поворот сторон 1'4' и 4'3' на равные по величине и противоположные по знаку углы g, так что окончательно элемент 1234 будет занимать положение 4'1"2"3" (рис. 12.3, г).

Тема №13. КРУЧЕНИЕ

Построение эпюр крутящих моментов

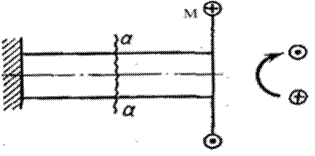
Стержень испытывает кручение, если в его поперечных сече­ниях возникают крутящие моменты, т. е. моменты, лежащие в плоскости сечения. Обычно эти крутящие моменты М_К возника­ют под действием внешних моментов (рис.13.1).

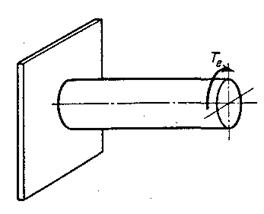
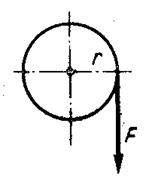
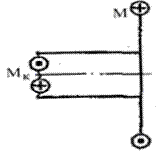
Однако и поперечная нагрузка, смещенная относительно оси стержня, вызывает крутящие моменты (рис. 13.2), но в указан­ном случае в поперечных сечениях наряду с крутящими момента­ми возникают и другие внутренние усилия – поперечные силы и изгибающие моменты.

Вместо аксонометрического изображения будем применять главным образом плоское, как более простое. Внешние скручивающие моменты и внутренние крутящие моменты будем изобра­жать в виде линии с двумя кружочками. В одном из них будем ставить точку, обозначающую начало стрелки (на нас), а в дру­гом – крестик, обозначающий конец стрелки, направленный от нас (рис. 13.3).

Дата добавления: 2013-12-12