При кручении деформации сдвига и касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения

Рис. 13.6.

Рис. 13.4. Рис. 13.5.

Рис. 13.3.

Для определения крутящих моментов М_К, возникающих в се­чениях вала под действием внешних скручивающих моментов или поперечной нагрузки, будем применять метод сечений. Сделаем мысленный разрез стержня (рис. 13.3), например по а – а, отбросим одну часть стержня, в данном слу­чае левую, и рассмотрим равно­весие оставшейся правой части.

Взаимодействие частей стер­жня заменим крутящим моментом М_К, уравновешивающим внешний момент М. Для равновесия отсе­ченной части необходимо, чтобы ал­гебраическая сумма всех моментов, действующих на нее, была равна нулю. Отсюда в рассматриваемом случае М = М_К. Если на отсеченную часть будет действовать несколько внешних моментов, то, проведя аналогичные рассуждения, можно убедиться, что крутящий момент в сечении численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения.

Для наглядного представления о характере распределения и значении крутящих моментов по длине стержня строят эпюры (графики) этих моментов. Построение их вполне аналогично построению эпюр продольных сил при растяжении или сжатии. Для построения эпюр необходимо условиться о правиле знаков. Общепринятого правила знаков для крутящих моментов не существует. Может быть принято любое правило знаков. Важно лишь принятое правило выдержать на всем протяжении эпюры.

Определение напряжений в стержнях круглого сечения

Крутящие моменты, о которых шла речь выше, представляют лишь равнодействующие внутренних сил. Фактически в попе­речном сечении скручиваемого стержня действуют непрерывно распределенные внутренние касательные напряжения, к опреде­лению которых теперь и перейдем.

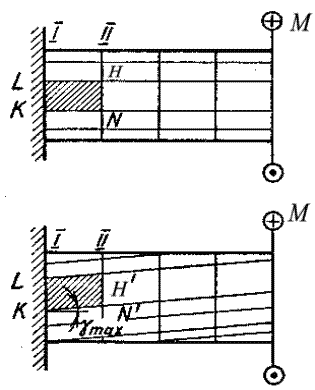
Ознакомимся прежде всего с результатами опытов. Если на поверхности стержня круглого сечения нанести прямоугольную сетку, то после деформации окажется (рис. 13.4):

1) прямоугольная сетка превратится в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений в поперечных сечениях бруса, а по закону парности касательных напряжений – и в продольных его сечениях;

2) расстояния между окружностями, например между I и II, не изменятся. Не изменятся длина стержня и его диаметр. Естес­твенно допустить, что каждое поперечное сечение поворачивает­ся в своей плоскости на некоторый угол как жесткое целое (гипотеза плоских и жестких сечений). На основании этой гипотезы можно считать, что радиусы всех поперечных сечений будут поворачиваться (на разные углы), оставаясь прямолиней­ными.

На основании этого можно принять, что при кручении в попе­речных сечениях стержня действуют только касательные напря­жения, т. е. напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг.

Формулы, полученные на основе этого допущения, подтвер­ждаются опытами. Точка D переместится по дуге DD', точка С — по меньшей дуге С С' (рис. 13.5).

На рис. 13.6 в более крупном масштабе изображена часть стерж­ня между сечениями I и II и показана одна сторона KN элемента KLHN (см. рис. 13.4).

В центре тяжести круглого сечения касательные напряжения равны нулю. Наибольшие касательные напряжения будут в точ­ках сечения, расположенных у поверхности стержня.

Формула для определения касательных напряжений при кручении имеет вид:

,

где I_р – полярный момент инерции сечения; r – произвольный радиус.

Как видно из этой формулы, в точках, одинаково удаленных от центра сечения, напряжения t одинаковы.

Наибольшие напряжения в точках у контура сечения:

, где .

Дата добавления: 2013-12-12